Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T09:49:11.666Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Dimensional Harmonic Volume Can be Computed as an Iterated Integral

Published online by Cambridge University Press:  20 November 2018

William M. Faucette
William M. Faucette*
Affiliation:
Division of Mathematics and Computer Science Northeast Missouri State University Kirksville, Missouri 63501 U. S. A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper it is shown that the computation of higher dimensional harmonic volume, defined in [1], can be reduced to Harris' computation in the onedimensional case (See [3]), so that higher dimensional harmonic volume may be computed essentially as an iterated integral. We then use this formula to produce a specific smooth curve 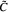, namely a specific double cover of the Fermat quartic, so that the image 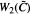of the second symmetric product of 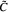in its Jacobian via the Abel-Jacobi map is algebraically inequivalent to the image of 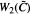under the group involution on the Jacobian.

Keywords

14H4014C10harmonic volumealgebraic equivalence
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 328 - 340
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Faucette, W., Harmonie Volume, Symmetric Products, and the Abel-Jacobi Map, Trans, of the Amer. Math. Soc, to appear.Google Scholar
2. Gross, B., On the Periods of Abelian Integrals and a Formula of Chowla and Selberg , Invent. Math. 45 193–211.Google Scholar
3. Harris, B., Harmonic Volumes , Acta Mathematica 150(1983) 91–123.Google Scholar
4. Harris, B., Homological versus algebraic equivalence in a Jacobian , Proc. Nat. Acad. Sci. U.S.A. 80(1983) 1157–1158.Google Scholar
5. Harris, B., A triple product for automorp hie forms , Quart. J. Math. Oxford 34(1983) 67–75.Google Scholar
6. Weil, A., Collected Papers , Oeuvres Scientifiques (2), 533–534.Google Scholar