No CrossRef data available.
Article contents
The Hermite–Joubert Problem and a Conjecture of Brassil and Reichstein
Published online by Cambridge University Press: 04 January 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We show that Hermite’s theorem fails for every integer 
$n$ of the form 
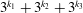$3^{k_{1}}+3^{k_{2}}+3^{k_{3}}$ with integers 
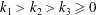$k_{1}>k_{2}>k_{3}\geqslant 0$. This confirms a conjecture of Brassil and Reichstein. We also obtain new results for the relative Hermite–Joubert problem over a finitely generated field of characteristic 0.
MSC classification
Primary:
11D72: Equations in many variables
Secondary:
11G05: Elliptic curves over global fields
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
Bennett, M. A.,
Effective measures of irrationality for certain algebraic numbers
. J. Austral. Math. Soc. Ser. A
62(1997), no.3, 329–344. https://doi.org/10.1017/S144678870000104X.Google Scholar
Bombieri, E. and Gubler, W.,
Heights in Diophantine geometry
. New Mathematical Monographs, 4. Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511542879.Google Scholar
Brassil, M. and Reichstein, Z.,
The Hilbert-Joubert problem over p-closed fields
. In: Algebraic groups, structure and actions, Proc. Sympos. Pure Math., 94, American Mathematical Society, RI, 2017.Google Scholar
Buhler, J. and Reichstein, Z.,
On the essential dimension of a finite group
. Compositio. Math.
106(1997), 159–179. https://doi.org/10.1023/A:1000144403695.Google Scholar
Coray, D. F.,
Cubic hypersurfaces and a result of Hermite
. Duke Math. J.
54(1987), 657–670. https://doi.org/10.1215/S0012-7094-87-05428-7.Google Scholar
Faltings, G.,
Diophantine approximation on abelian varieties
. Ann. of Math. (2)
133(1991), no. 3, 549–576. https://doi.org/10.2307/2944319.Google Scholar
Faltings, G.,
The general case of S. Lang’s conjecture
. In: Barsotti Symposium in Algebraic Geometry (Abano Terme, 1991), Perspect. Math., 15, Academic Press, San Diego, CA, 1994, pp. 175–182.10.1016/B978-0-12-197270-7.50012-7Google Scholar
Hermite, C.,
Sur l’invariant du 18
e
ordre des formes du cinquième degré et sur le rôle qu’il joue dans la résolution de l’équation du cinquième degré, extrait de deux lettres de M. Hermite á léditeur
. J. Reine Angew. Math.
59(1861), 304–305. https://doi.org/10.1515/crll.1861.59.304.Google Scholar
Joubert, P.,
Sur l’equation du sixième degré
. C. R. Acad. Sci. Paris
64(1867), 1025–1029.Google Scholar
Kraft, H.,
A result of Hermite and equations of degree 5 and 6
. J. Algebra
297(2006), 234–253. https://doi.org/10.1016/j.jalgebra.2005.04.015.Google Scholar
Lang, S., Fundamentals of diophantine geometry. Springer-Verlag, New York, 1983. https://doi.org/10.1007/978-1-4757-1810-2.Google Scholar
McQuillan, M.,
Division points on semi-abelian varieties
. Invent. Math.
120(1995), 143–159. https://doi.org/10.1007/BF01241125.Google Scholar
Reichstein, Z.,
On a theorem of Hermite and Joubert
. Canad. J. Math.
51(1999), 69–95. https://doi.org/10.4153/CJM-1999-005-x.Google Scholar
Reichstein, Z. and Youssin, B.,
Conditions satisfied by characteristic polynomials in fields and division algebras
. J. Pure Appl. Algebra
166(2002), 165–189. https://doi.org/10.1016/S0022-4049(01)00009-3.Google Scholar
Selmer, E. S.,
The diophantine equation ax
3 + by
3 + cz
3 = 0
. Acta Math.
85(1951), 203–362. https://doi.org/10.1007/BF02395746.Google Scholar
Silverman, J. H.,
The difference between the Weil height and the canonical height on elliptic curves
. Math. Comp.
55(1990), 723–743. https://doi.org/10.2307/2008444.Google Scholar
Silverman, J. H., The Arithmetic of elliptic curves. Second ed., Graduate Texts in Mathematics, 106, Springer, Dordrecht, 2009.Google Scholar
Vojta, P.,
Integral points on subvarieties of semiabelian varieties. I
. Invent. Math.
126(1996), no. 1, 133–181. https://doi.org/10.1007/s002220050092.Google Scholar
You have
Access