Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-20T16:19:28.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Helices, Hasimoto Surfaces and Bäcklund Transformations

Published online by Cambridge University Press:  20 November 2018

Thomas A. Ivey
Thomas A. Ivey*
Affiliation:
Department of Mathematics, College of Charleston, Charleston, SC 29464-0001, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Travelling wave solutions to the vortex filament flow generated by elastica produce surfaces in 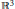${{\mathbb{R}}^{3}}$ that carry mutually orthogonal foliations by geodesics and by helices. These surfaces are classified in the special cases where the helices are all congruent or are all generated by a single screw motion. The first case yields a new characterization for the Bäcklund transformation for constant torsion curves in 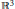${{\mathbb{R}}^{3}}$, previously derived fromthe well-known transformation for pseudospherical surfaces. A similar investigation for surfaces in 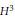${{H}^{3}}$ or 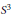${{S}^{3}}$ leads to a new transformation for constant torsion curves in those spaces that is also derived from pseudospherical surfaces.

Keywords

53A0558F3752C4258A15surfacesfilament flowBäcklund transformations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 4 , 01 December 2000 , pp. 427 - 439
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Bianchi, L., Sopra le deformazioni isogonali delle superficie a curvatura constante in geometria ellitica ed iperbolica. Annali di Matem. (3) 18 (1911), 185–243.Google Scholar
[2] Bryant, R., Chern, S.-S., Gardner, R., Goldschmidt, H. and Griffiths, P., Exterior Differential Systems. Math. Sci. Res. Inst. Publ. 18, Springer-Verlag, New York, 1991.Google Scholar
[3] Calini, A. and Ivey, T., Bäcklund transformations and knots of constant torsion. J. Knot Theory Ramifications, to appear.Google Scholar
[4] Chern, S.-S. and Terng, C.-L., An analogue of Bäcklund's theorem in affine geometry. Rocky Mountain Math J. 10 (1980), 105–124.Google Scholar
[5] Eisenhart, L. P., A Treatise on the Differential Geometry of Curves and Surfaces. Ginn, 1909.Google Scholar
[6] Hasimoto, H., Motion of a vortex filament and its relation to elastica. J. Phys. Soc. Japan 31 (1971), 293.Google Scholar
[7] Hasimoto, H., A soliton on a vortex filament. J. Fluid Mech. 51 (1972), 477.Google Scholar
[8] Langer, J. and Perline, R., Local Geometric Invariants of Integrable Evolution Equations. J. Math. Phys. 35 (1994), 1732–1737.Google Scholar
[9] Langer, J. and Singer, D., Lagrangian Aspects of the Kirchhoff Elastic Rod. SIAM Reviews 38 (1996), 605–618.Google Scholar
[10] Ricca, R., The contributions of Da Rios and Levi-Civita to asymptotic potential theory and vortex filament dynamics. Fluid Dynam. Res. 18 (1996), 245–268.Google Scholar
[11] Rogers, C., Bäcklund transformations in soliton theory. In: Soliton theory: a survey of results (ed. A. P. Fordy), St. Martin's Press, 1990, 97–130.Google Scholar
[12] Tenenblat, K., Bäcklund's theorem for submanifolds of space forms and a generalized wave equation. Bol. Soc. Brasil. Mat. 16 (1985), 67–92.Google Scholar
[13] Tenenblat, K. and Terng, C.-L., Bäcklund theorem for n-dimensional submanifolds of R2n−1 . Annals of Math. 111 (1980), 477–490.Google Scholar