Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T05:51:48.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc

Part of: General theory of linear operators Series expansions Special classes of linear operators

Published online by Cambridge University Press:  11 June 2020

Augustin Mouze  and
Vincent Munnier
Augustin Mouze*
Affiliation:
École Centrale de Lille, CNRS, UMR 8524 - Laboratoire Paul Painlevé, F-59000 Lille, France
Vincent Munnier
Affiliation:
Lycée Jacques Prévert, 163 rue de Billancourt, 92100 Boulogne Billancourt, France e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For any 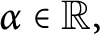$\alpha \in \mathbb {R},$ we consider the weighted Taylor shift operators 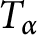$T_{\alpha }$ acting on the space of analytic functions in the unit disc given by 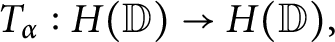$T_{\alpha }:H(\mathbb {D})\rightarrow H(\mathbb {D}),$

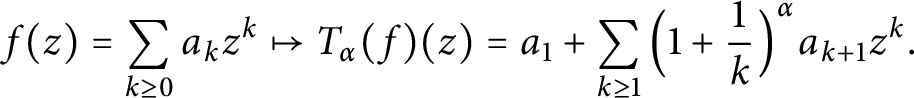$$ \begin{align*}f(z)=\sum_{k\geq 0}a_{k}z^{k}\mapsto T_{\alpha}(f)(z)=a_1+\sum_{k\geq 1}\Big(1+\frac{1}{k}\Big)^{\alpha}a_{k+1}z^{k}.\end{align*}$$
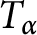We establish the optimal growth of frequently hypercyclic functions for $T_\alpha $ in terms of 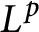$L^p$ averages, 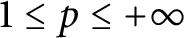$1\leq p\leq +\infty $ . This allows us to highlight a critical exponent.

Keywords

Frequently hypercyclic operatorTaylor shiftboundary behavior

MSC classification

Primary: 47A16: Cyclic vectors, hypercyclic and chaotic operators
Secondary: 47B38: Operators on function spaces (general) 30B30: Boundary behavior of power series, over-convergence
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 2 , June 2021 , pp. 264 - 281
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partly supported by the grant ANR-17-CE40-0021 of the French National Research Agency ANR (project Front).

References

Bayart, F. and Grivaux, S., Hypercyclicité: le rôle du spectre ponctuel unimodulaire . C. R. Acad. Sci. Paris. 338(2004), 703–708. https://doi.org/10.1016/j.crma.2004.02.012 CrossRefGoogle Scholar
Bayart, F. and Grivaux, S., Frequently hypercyclic operators . Trans. Amer. Math. Soc. 358(2006), 5083–5117. https://doi.org/10.1090/S0002-9947-06-04019-0 CrossRefGoogle Scholar
Bayart, F. and Matheron, E., Dynamics of linear operators . Cambridge Tracts in Mathematics, 179, Cambridge University Press, Cambridge, 2000. https://doi.org/10.1017/CB09780511581113 Google Scholar
Beise, H. P., Meyrath, T., and Müller, J., Mixing Taylor shifts and universal Taylor series . Bull. London Math. Soc. 47(2015), 136–142. https://doi.org/10.1112/blms/bdu104 CrossRefGoogle Scholar
Blasco, O., Bonilla, A., and Grosse Erdmann, K-G., Rate of growth of frequently hypercyclic functions . Proc. Edinb. Math. Soc. 53(2010), 39–59. https://doi.org/10.1017/S0013091508000564 CrossRefGoogle Scholar
Drasin, D., and Saksman, E., Optimal growth of frequently hypercyclic entire functions . J. Funct. Anal. 263(2012), 3674–3688. https://doi.org/10.1016/j.jfa.2012.09.007 CrossRefGoogle Scholar
Duren, P. L., Theory of $H^p$ spaces. Pure and Applied Mathematics, 38, Academic Press, New York and London, 1970.Google Scholar
Edwards, R. E. and Gaudry, G. I., Littlewood–Paley and multiplier theory . Ergebnisse der Mathematik und ihrer Grenzgebiete, 90, Springer-Verlag, Berlin and New York, 1977.Google Scholar
Girela, D. and Peláez, J. A., Integral means of analytic functions . Ann. Acad. Sci. Fenn. Math. 29(2004), 459–469.Google Scholar
Grosse Erdmann, K-G. and Peris, A., Linear chaos . Universitext, Springer, London, 2011. https://doi.org/10.1007/978-1-4471-2170-1 Google Scholar
Mouze, A. and Munnier, V., Frequent hypercyclicity of random holomorphic functions for Taylor shifts and optimal growth. J. Anal. Math., to appear.Google Scholar
Rudin, W., Some theorems on Fourier coefficients . Proc. Amer. Math. Soc. 10(1959), 855–859. https://doi.org/10.2307/2033608 CrossRefGoogle Scholar
Samko, S. G., Kilbas, A. A., and Marichev, O. I., Fractional integrals and derivatives . In: Theory and applications, Gordon and Breach Science Publishers, Yverdon, 1993.Google Scholar
Thelen, M., Frequently hypercyclic Taylor shifts . Comput. Methods Funct. Theory 17(2017), 129–138. https://doi.org/10.1007/s40315-016-0173-z CrossRefGoogle Scholar