Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:46:19.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Griffiths Groups of Supersingular Abelian Varieties

Published online by Cambridge University Press:  20 November 2018

B. Brent Gordon  and
Kirti Joshi
B. Brent Gordon
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, Oklahoma, 73019 U.S.A., e-mail: [email protected]
Kirti Joshi
Affiliation:
Department of Mathematics, University of Arizona, Tucson, Arizona, 85721, U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Griffiths group 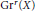$\text{G}{{\text{r}}^{r}}\left( X \right)$ of a smooth projective variety 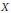$X$ over an algebraically closed field is defined to be the group of homologically trivial algebraic cycles of codimension $r$ on 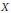$X$ modulo the subgroup of algebraically trivial algebraic cycles. The main result of this paper is that the Griffiths group 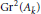$\text{G}{{\text{r}}^{2}}\left( {{A}_{{\bar{k}}}} \right)$ of a supersingular abelian variety 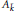${{A}_{{\bar{k}}}}$ over the algebraic closure of a finite field of characteristic 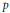$p$ is at most a 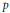$p$-primary torsion group. As a corollary the same conclusion holds for supersingular Fermat threefolds. In contrast, using methods of 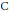$\text{C}$. 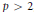Schoen it is also shown that if the Tate conjecture is valid for all smooth projective surfaces and all finite extensions of the finite ground field $k$ of characteristic $p\,>\,2$, then the Griffiths group of any ordinary abelian threefold ${{A}_{{\bar{k}}}}$ over the algebraic closure of $k$ is non-trivial; in fact, for all but a finite number of primes 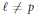$\ell \,\ne \,p$ it is the case that 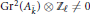$\text{G}{{\text{r}}^{2}}\left( {{A}_{{\bar{k}}}} \right)\,\otimes \,{{\mathbb{Z}}_{\ell }}\,\ne \,0$.

Keywords

14J2014C25Griffiths groupBeauville conjecturesupersingular Abelian varietyChow group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 213 - 219
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Beauville, A., Sur l’anneau de Chow d’une variété abélienne. Math. Ann. (4) 273 (1986), 273–1986.Google Scholar
[2] Bloch, S., Torsion algebraic cycles and a theorem of Roitman. Compositio Math. 39 (1979), 39–1979.Google Scholar
[3] Bloch, S., Lectures on algebraic cycles. Duke University Math., Duke University Press, 1980.Google Scholar
[4] Colliot-Thélène, J.-L., Sansuc, J.-J. and Soulé, Ch., Torsion dans le groupe de Chow de codimension deux. Duke Math. J. (3) 50 (1983), 50–1983.Google Scholar
[5] Colliot-Thélène, J.-L. and Raskind, W., Groupe de Chow de codimension deux des variétès définies sur un corps de nombres: un théorème de finitude pour la torsion. Invent. Math. 105 (1991), 105–1991.Google Scholar
[6] Deninger, C. and Murre, J., Motivic decomposition of abelian schemes and the Fourier transform. J. Reine Angew. Math. 422 (1991), 422–1991.Google Scholar
[7] Gros, M. and Suwa, N., Application d’Abel-Jacobi p-adique et cycles algébriques. Duke Math. J. (2) 57, 578–613.Google Scholar
[8] Gouvea, F. and Yui, N., Arithmetic of diagonal hypersurfaces over finite fields. London Math. Soc. Lecture Notes 209, Cambridge University Press, Cambridge, 1995.Google Scholar
[9] Fakhruddin, N., Remarks on the Chow groups of supersingular varieties. Canad. Math. Bull., 45 (2002), 45–2002.Google Scholar
[10] Jannsen, U., Mixed motives and algebraic K-theory. Lecture Notes in Math. 1400, Springer-Verlag, Berlin, 1990.Google Scholar
[11] Katz, N., Some consequences of the Riemann hypothesis for varieties over finite fields. Invent. Math. 23 (1974), 23–1974.Google Scholar
[12] Katz, N., Slope filtration of F-crystals. Astérisque 63(1979).Google Scholar
[13] Künneman, K., A Lefschetz decomposition for Chow motives of abelian schemes. Invent. Math. (1) 113 (1993), 113–1993.Google Scholar
[14] Merkur’ev, A. S. and Suslin, A. A., k-cohmology of Severi-Brauer varieties and the norm residue homomorphism. Math. USSR-Izv. 21 (1983), 21–1983.Google Scholar
[15] Mukai, S., Duality between D(X) and D(X) with its applications to Picard sheaves. NagoyaMath. J. 81 (1981), 81–1981.Google Scholar
[16] Oort, F., Subvarieties of moduli spaces. Invent. Math. 24 (1974), 24–1974.Google Scholar
[17] Oort, F., Lifting algebraice curves, abelian varieties and their endomorphisms. Algebraic Geometry, Proceedings Symp. Pure Math. 46, Vol II, 165–195, 1987.Google Scholar
[18] Raskind, W., A finiteness theorem in the Galois cohomology of algebraic number fields. Trans. Amer. Math. Soc. 63 (1986), 63–1986.Google Scholar
[19] Schoen, C., On the computation of the cycle class map for nullhomologous cycles over the algebraic closure of a finite field. Ann. Sci. École Norm. Sup. (4) 28 (1995), 28–1995.Google Scholar
[20] Schoen, C., On the image of the l-adic Abel-Jacobi map for a variety over the algebraic closure of a finite field. J. Amer. Math. Soc. (3) 12 (1999), 12–1999.Google Scholar
[21] Soulé, C., Groupes de Chow et K-théorie de variétés sur un corps fini.Math. Ann. 268 (1984), 268–1984.Google Scholar
[22] Suwa, N., Sur l’image de l’application d’Abel-Jacobi de Bloch. Bull. Soc. Math. France 116 (1988), 116–1988.Google Scholar
[23] Tate, J., Algebraic cycles and poles of zeta functions. In Arithmetical Algebraic Geometry (Proc. Conf. Purdue. Univ), pages 93–110, Purdue Univ., Harper & Row, New York, 1965.Google Scholar