Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T21:50:23.091Z Has data issue: false hasContentIssue false
  • English
  • Français

A Geometric Approach to Voiculescu-Brown Entropy

Published online by Cambridge University Press:  20 November 2018

David Kerr
David Kerr*
Affiliation:
Mathematisches Institut Westfälische Wilhelms-Universität Münster Einsteinstraß 62 48149 Münster Germany, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A basic problem in dynamics is to identify systems with positive entropy, i.e., systems which are “chaotic.” While there is a vast collection of results addressing this issue in topological dynamics, the phenomenon of positive entropy remains by and large a mystery within the broader noncommutative domain of 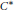${{C}^{*}}$-algebraic dynamics. To shed some light on the noncommutative situation we propose a geometric perspective inspired by work of Glasner and Weiss on topological entropy. This is a written version of the author’s talk at the Winter 2002 Meeting of the Canadian Mathematical Society in Ottawa, Ontario.

Keywords

46L5537B40
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 4 , 01 December 2004 , pp. 553 - 565
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Adler, R. L., Konheim, A. G., and McAndrew, M. H.. Topological entropy. Trans. Amer.Math. Soc. 114 (1965), 309–319.Google Scholar
[2] Blanchard, F., A disjointness theorem involving topological entropy. Bull. Soc. Math. France 121 (1993), 465–478.Google Scholar
[3] Boca, F. P. and Goldstein, P., Topological entropy for the canonical endomorphism of Cuntz-Krieger algebras. Bull. LondonMath. Soc. 32 (2000), 345–352.Google Scholar
[4] Bowen, R., Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
[5] Brown, N. P., Topological entropy in exact C*-algebras. Math. Ann. 314 (1999), 347–367.Google Scholar
[6] Brown, N. P. and Choda, M., Approximation entropies in crossed products with an application to free shifts. Pacific J. Math. 198 (2001), 331–346.Google Scholar
[7] Brown, N. P., Dykema, K. and Shlyakhtenko, D., Topological entropy of free product automorphisms. Acta Math. 189 (2002), 1–35.Google Scholar
[8] Choda, M., Entropy of Cuntz's canonical endomorphism. Pacific J. Math. 190 (1999), 235–245.Google Scholar
[9] Denker, M., Grillenberger, C. and Sigmund, K., Ergodic Theory on Compact Spaces. Lecture Notes in Mathematics 527, Springer-Verlag, Berlin, 1976.Google Scholar
[10] Dinaburg, E. I., The relation between topological entropy and metric entropy. Soviet Math. Dokl. 11 (1969), 13–16.Google Scholar
[11] Dykema, K., Topological entropy of some automorphisms of reduced amalgamated free product C*-algebras. Ergodic Theory Dynamical Systems 21 (2001), 1683–1693.Google Scholar
[12] Dykema, K. and Shlyakhtenko, D., Exactness of Cuntz-Pimsner C*-algebras. Proc. EdinburghMath. Soc. 44 (2001), 425–444.Google Scholar
[13] Glasner, E. and Weiss, B., Quasi-factors of zero entropy systems. J. Amer.Math. Soc. 8 (1995), 665–686.Google Scholar
[14] Haagerup, U. and Pisier, G., Bounded linear operators between C*-algebras. Duke Math. J. 71 (1993), 889–925.Google Scholar
[15] Hasselblatt, B. and Katok, A., Introduction to the Modern Theory of Dynamical Systems. Encyclopedia of Mathematics and its Applications 54, Cambridge University Press, Cambridge, 1995.Google Scholar
[16] Hiai, F. and Petz, D., The Semicircle Law, Free Random Variables and Entropy. Mathematical Survey and Monographs 77, American Mathematical Society, Providence, RI, 2000.Google Scholar
[17] Kerr, D. and Li, H., Positive Voiculescu-Brown entropy in noncommutative toral automorphisms. arXiv:math.OA/0303090, 2003.Google Scholar
[18] Kerr, D., Entropy and induced dynamics on state spaces, to appear in Geom. Funct. Anal. arXiv:math.OA/0302118 v3, 2003.Google Scholar
[19] Kerr, D., Pressure for automorphisms of exact C*-algebras and a noncommutative variational principle. Ph.D. thesis, University of Toronto, 2001.Google Scholar
[20] Kerr, D. and Pinzari, C., Noncommutative pressure and the variational principle in Cuntz-Krieger-type C*-algebras. J. Funct. Anal. 188 (2002), 156–215.Google Scholar
[21] Kirchberg, E., On subalgebras of the CAR-algebra. J. Funct. Anal. 129 (1995), 35–63.Google Scholar
[22] Kurlberg, P. and Rudnick, Z., Value distribution for eigenfunctions of desymmetrized quantum maps. Internat.Math. Res. Notices. (2001), 985–1002.Google Scholar
[23] Kurlberg, P. and Rudnick, Z., On quantum ergodicity for linear maps of the torus. Comm. Math. Phys. 222 (2001), 201–227.Google Scholar
[24] Kurlberg, P. and Rudnick, Z., Hecke theory and equidistribution for the quantization of the linear maps of the torus. Duke Math. J. 103 (2000), 47–77.Google Scholar
[25] Narnhofer, H. and Thirring, W., C*-dynamical systems that are asymptotically highly anticommutative. Lett. Math. Phys. 35 (1995), 145–154.Google Scholar
[26] Neshveyev, S. and Størmer, E., The variational principle for a class of asymptotically abelian C*-algebras. Comm. Math. Phys. 215 (2000), 177–196.Google Scholar
[27] Paulsen, V. I., Completely bounded maps and dilations. Pitman Research Notes in Mathematics 146, Longman, 1986.Google Scholar
[28] Pisier, G., Non-commutative vector valued Lp-spaces and completely p-summing maps. Astérisque 247 (1998).Google Scholar
[29] Pisier, G., The operator Hilbert space OH, complex interpolation and tensor norms. Mem. Amer. Math. Soc. 122(1996).Google Scholar
[30] Pisier, G., Exact operator spaces. In: Recent advances in operator algebras (Orléans 1992). Astérisque 232 (1995), 159–186.Google Scholar
[31] Pop, C. and Smith, R. R., Crossed products and entropy of automorphisms. J. Funct. Anal. 206 (2004), 210–232.Google Scholar
[32] Popa, S., Maximal injective subalgebras in factors associated with free groups. Adv. Math. 50 (1983), 27–48.Google Scholar
[33] Størmer, E., A survey of noncommutative dynamical entropy. In: Classification of Nuclear C*-algebras. Entropy in Operator Algebras, Springer, Berlin, 2002, pp. 147–198.Google Scholar
[34] Størmer, E., Entropy of some automorphisms of the II1-factor of the free group in infinite number of generators. Invent.Math. 110 (1992), 63–73.Google Scholar
[35] Tomczak-Jaegermann, N., The moduli of smoothness and convexity and the Rademacher averages of trace classes Sp (1 ≤ p < ∞). Studia Math. 50 (1974), 163–182.Google Scholar
[36] Voiculescu, D. V., Dynamical approximation entropies and topological entropy in operator algebras. Comm. Math. Phys. 170 (1995), 249–281.Google Scholar
[37] Voiculescu, D. V., Noncommutative random variables and spectral problems in free product C*-algebras. Rocky Mountain J. Math. 20 (1990), 263–283.Google Scholar
[38] Voiculescu, D. V., Dykema, K. J. and Nica, A., Free Random Variables. A Noncommutative Probability Approach to Free Products with Applications to Random Matrices, Operator Algebras and Harmonic Analysis on Free Groups. CRMMonograph Series 1, American Mathematical Society, Providence, RI, 1992.Google Scholar
[39] Weaver, N., Mathematical Quantization. Studies in Advanced Mathematics. Chapman & Hall/CRC, Boca Raton, FL, 2001.Google Scholar
[40] Zelditch, S., Index and dynamics of quantized contact transformations. Ann. Inst. Fourier (Grenoble) 47 (1997), 305–363.Google Scholar