Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T17:31:51.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Geodesic Correspondence in the Brans-Dicke Theory

Published online by Cambridge University Press:  20 November 2018

B. O. J. Tupper
B. O. J. Tupper*
Affiliation:
University of New Brunswick Fredericton, New Brunswick
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent article [1] vacuum field solutions of the Brans-Dicke [2] field equations were found, the space-time metric in each solution being of the Friedmann type. Most of these solutions existed only for specific values of the parameter ω and, in particular, the two largest sets of solutions corresponded to the values 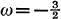and 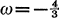. Peters [3, 4] has shown that when 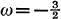all solutions of the Brans-Dicke vacuum equations are conformai to space-times with vanishing Ricci tensor. The purpose of this note is to investigate the possible geometric consequences of the value .

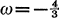Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 151 - 153
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. O'Hanlon, J. and Tupper, B. O. J., Vacuum-field solutions in the Brans-Dicke theory, II Nuovo Cimento 7B (1972), 305-312.Google Scholar
2. Brans, C. and Dicke, R. H., Mach's principle and a relativistic theory of gravitation, Phys. Rev. 124 (1961), 925-935.Google Scholar
3. Peters, P. C., Conformai invariance and geometrization of the Hoyle-Narlikar mass field, Phys. Lett. 20 (1966), 641-642.Google Scholar
4. Peters, P. C., Geometrization of the Brans-Dicke scalar field, Journ. Math. Phys., 10 (1969), 1029-1031.Google Scholar
5. Eisenhart, L. P., Riemannian Geometry, Princeton Univ. Press, 1925.Google Scholar
6. Petrov, A. Z., Einstein Spaces, Pergamon, 1969.Google Scholar