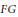Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sehgal, S. K.
and
Zaicev, M. V.
2005.
Identities of Group Algebras.
Communications in Algebra,
Vol. 33,
Issue. 11,
p.
4283.
Barrett, John W.
and
Tavares, Sara O. G.
2015.
Two-Dimensional State Sum Models and Spin Structures.
Communications in Mathematical Physics,
Vol. 336,
Issue. 1,
p.
63.