Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T16:47:57.687Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalized Characterization of Commutators of Parabolic Singular Integrals

Published online by Cambridge University Press:  20 November 2018

Steve Hofmann ,
Xinwei Li  and
Dachun Yang
Steve Hofmann
Affiliation:
Department of Mathematics, University of Missouri Columbia Columbia, Missouri 65211, U.S.A., email: [email protected]
Xinwei Li
Affiliation:
Department of Mathematics, Washington University, St. Louis, Missouri 63130-4899 U.S.A., email: [email protected]
Dachun Yang
Affiliation:
Department of Mathematics Washington University St. Louis, Missouri 63130-4899 U.S.A., email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 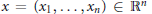$x\,=\,\left( {{x}_{1}},\,.\,.\,.\,,\,{{x}_{n}} \right)\,\in \,{{\mathbb{R}}^{n}}$ and 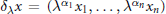${{\delta }_{\text{ }\!\!\lambda\!\!\text{ }}}x\,=\,\left( {{\text{ }\!\!\lambda\!\!\text{ }}^{{{\alpha }_{1}}}}{{x}_{1}},\,.\,.\,.\,,\,{{\text{ }\!\!\lambda\!\!\text{ }}^{{{\alpha }_{n}}}}{{x}_{n}} \right)$, where 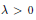$\text{ }\lambda \,>\text{0}$ and 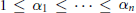$1\,\le \,{{\alpha }_{1}}\,\le \,\cdot \,\cdot \,\cdot \,\le \,{{\alpha }_{n}}$. Denote 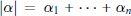$\left| \alpha \right|\,=\,{{\alpha }_{1}}+\,\cdot \,\cdot \,\cdot \,+{{\alpha }_{n}}$. We characterize those functions 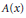$A\left( x \right)$ for which the parabolic Calderón commutator

1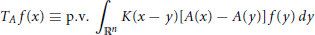

$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{T}_{A}}f\left( x \right)\equiv \text{p}\text{.v}\text{.}\int_{{{\mathbb{R}}^{n}}}{K\left( x-y \right)\left[ A\left( x \right)-A\left( y \right) \right]}f\left( y \right)dy$$

is bounded on 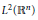${{L}^{2}}\left( {{\mathbb{R}}^{n}} \right)$, where 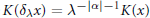$K\left( {{\delta }_{\text{ }\!\!\lambda\!\!\text{ }}}x \right)\,=\,{{\text{ }\!\!\lambda\!\!\text{ }}^{-\,\left| \alpha \right|\,-\,1}}K\left( x \right)$, 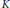$K$ is smooth away fromthe origin and satisfies a certain cancellation property.

Keywords

42B20parabolic singular integralcommutatorparabolic BMO sobolev spacehomogeneous spaceT1-theoremsymbol
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 4 , 01 December 1999 , pp. 463 - 477
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Calderón, A. P., Commutators of singular integral operators. Proc.Nat. Acad. Sci. U.S.A. 74 (1977), 1324–1327.Google Scholar
[2] Calderón, A. P., An atomic decomposition of distributions in parabolic Hp spaces. Adv.Math. 25 (1977), 216–225.Google Scholar
[3] Calderón, A. P. and Torchinsky, A., Parabolic maximal functions associated with a distribution. Adv. Math. 16 (1975), 1–64.Google Scholar
[4] Calderón, A. P., Parabolic maximal functions associated with a distribution II. Adv. Math. 24 (1977), 101–171.Google Scholar
[5] Coifman, R. and Dahlberg, B., Singular integral characterizations of non-isotropic Hp spaces and the F. and M. Riesz theorem. In: Harmonic Analysis in Euclidean Spaces (eds. G. Weiss and S. Wainger), Proc. Symp. Pure Math. 35 (1979), 231–234.Google Scholar
[6] Coifman, R. and Meyer, Y., Non-linear harmonic analysis, operator theory, and P. D. E. Beijing Lectures in Harmonic Analysis (ed. E. M. Stein), Princeton Univ. Press, Princeton, New Jersey, 1986, 3–45.Google Scholar
[7] Coifman, R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homog`enes. Lecture Notes in Math. 242, Springer-Verlag, Berlin, 1971.Google Scholar
[8] David, G. and Journ´e, J. L., A boundedness criterion for generalized Calder´on-Zygmund operators. Ann. of Math. 120 (1984), 371–397.Google Scholar
[9] Fabes, E. B. and Riviere, N. M., Singular integrals with mixed homogeneity. Studia Math. 27 (1966), 19–38.Google Scholar
[10] Fabes, E. B. and Riviere, N. M., Symbolic calculus of kernels with mixed homogeneity. Singular Integrals (ed. A. P. Calder ´ on), Proc. Symp. Pure Math. 10, Amer. Math. Soc., Providence, Rhode Island, 1967, 106–127.Google Scholar
[11] Fefferman, C. and Stein, E. M., Hp spaces of several variables. Acta Math. 129 (1972), 137–193.Google Scholar
[12] Garc´ia-Cuerva, J. and Rubio de Francia, J. L., Weighted Norm Inequalities and Related Topics. Math. Studies 116, North-Holland, New York, 1985.Google Scholar
[13] Hofmann, S., A characterization of commutators of parabolic singular integrals. Fourier Analysis and Partial Differential Equations (eds. J. Garc´ıa-Cuerva, E. Hern´andez, F. Soria and J.-L. Torrea), Stud. Adv. Math., CRC Press, Boca Raton, 1995, 195–210.Google Scholar
[14] Lewis, J. L. and Murray, M. A. M., Themethod of layer potentials for the heat equation in time-varying domains. Mem. Amer. Math. Soc. (545) 114, Amer.Math. Soc., Providence, Rhode Island, 1995.Google Scholar
[15] Meyers, N., Mean oscillation over cubes and H¨older continuity. Proc. Amer. Math. Soc. 15 (1964), 717–721.Google Scholar
[16] Murray, M. A. M., Commutators with fractional differentiation and BMO Sobolev spaces. Indiana Univ. Math. J. 34 (1985), 205–215.Google Scholar
[17] Peral, J. and Torchinsky, A., Multipliers in Hp(Rn), 0 < p < 1. Ark. Mat. 17 (1978), 225–234.Google Scholar
[18] Stein, E. M., Singular Integrals and Differentiability Properties of Functions. Princeton Univ. Press, Princeton, New Jersey, 1970.Google Scholar
[19] Strichartz, R., Bounded mean oscillation and Sobolev spaces. Indiana Univ.Math. J. 29 (1980), 539–558.Google Scholar