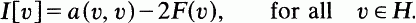Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-26T06:51:27.008Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of the Lax-Milgram Lemma

Published online by Cambridge University Press:  20 November 2018

K. Inayatnoor  and
M. Aslam Noor
K. Inayatnoor
Affiliation:
Mathematics Department Kerman University Kerman, Iran
M. Aslam Noor
Affiliation:
Mathematics Department Kerman University Kerman, Iran
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a real Hilbert space with its dual space H'. The norm and inner product in H are denoted by ||.|| and 〈.,.〉 respectively. We denote by 〈.,.〉, the pairing between H' and H.

If a(u, v) is a bilinear form and F is a real-valued continuous functional on H, then we consider I[v], a functional defined by

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 2 , 01 June 1980 , pp. 179 - 184
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Bers, L., John, F. and Schechter, M., Partial differential equations, Academic Press, New York, 1966.Google Scholar
2. Lax, P. D. and Milgram, A. N., Parabolic equations, Annals of Math. Study No. 33, Princeton, N.J., (1954), 167-190.Google Scholar
3. Lions, J. and Stampacchia, G.,Variational inequalities, Comm. Pure Apl. Math., 20 (1967), 493-518.Google Scholar
4. Noor, M.Aslam, Variational inequalities and approximation, TR/37, Mathematics Department, Brunei University, 1974.Google Scholar
5. Noor, M.Aslam and Whiteman, J. R., Error bounds for finite element solutions of mildly nonlinear elliptic boundary value problems, Num. Math. 26 (1976), 107-116.Google Scholar
6. Strang, G. and Fix, G., An analysis of the finite element method, Prentice-Hall Inc., Englewood Cliff, N.J. 1973.Google Scholar