Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T21:39:39.926Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of Integrality

Published online by Cambridge University Press:  20 November 2018

Jim Coykendall  and
Tridib Dutta
Jim Coykendall
Affiliation:
Department of Mathematics, North Dakota State University, Fargo, ND, U.S.A. e-mail: [email protected] [email protected]
Tridib Dutta
Affiliation:
Department of Mathematics, North Dakota State University, Fargo, ND, U.S.A. e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we explore a generalization of the notion of integrality. In particular, we study a near-integrality condition that is intermediate between the concepts of integral and almost integral. This property (referred to as the 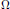$\Omega $-almost integral property) is a representative independent specialization of the standard notion of almost integrality. Some of the properties of this generalization are explored in this paper, and these properties are compared with the notion of pseudo-integrality introduced by Anderson, Houston, and Zafrullah. Additionally, it is shown that the 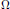$\Omega $-almost integral property serves to characterize the survival/lying over pairs of Dobbs and Coykendall.

Keywords

13B2213G0513B21integral closurecomplete integral closure
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 639 - 653
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Anderson, D. F., Houston, E., and Zafrullah, M., Pseudo-integrality. Canad. Math. Bull. 34(1991), no. 1, 15–22.Google Scholar
[2] Bourbaki, N., Elements of mathematics. Commutative algebra. Addision-Wesley Publishing Co., Reading, Mass., 1972.Google Scholar
[3] Coykendall, J., A characterization of polynomial rings with the half-factorial property. In: Factorization in integral domains (Iowa City, IA, 1996), Lecture Notes in Pure and Appl. Math., 189, Dekker, New York, pp. 291–294.Google Scholar
[4] Coykendall, J. and Dobbs, D. E., Survival-pairs of commutative rings have the lying-over property. Comm. Algebra. 31(2003), no. 1, 259–270. doi:10.1081/AGB-120016758Google Scholar
[5] Dobbs, D. E., Lying-over pairs of commutative rings. Canad. J. Math. 33(1981), no. 2, 454–475.Google Scholar
[6] Gilmer, R., Multiplicative ideal theory. Pure and Applied Mathematics, 12, Marcel Dekker, New York, 1972.Google Scholar
[7] Gilmer, R. and Heinzer, W., On the complete integral closure of an integral domain. J. Austral. Math. Soc. 6(1966), 351–361. doi:10.1017/S1446788700004304Google Scholar
[8] Kaplansky, I., Commutative rings. Revised ed., The University of Chicago Press, Chicago, IL, 1974.Google Scholar