Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T18:38:58.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalization of a Result of E. Lucas

Published online by Cambridge University Press:  20 November 2018

R. A. Macleod
R. A. Macleod*
Affiliation:
University of Victoria Victoria, British ColumbiaV8W 2Y2
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A well-known result of E. Lucas enables one to obtain the residue modulo p of 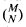in terms of the base-p digits of M and N. Using a recent result of P. W. Haggard and J. O. Kiltenen, a proof of N. J. Fine has been adapted to yield the corresponding residue modulo pr.

Keywords

11B4811B64
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 1 , 01 March 1988 , pp. 95 - 98
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Dwork, B., p-adic cycles, Inst. Hautes Études Sci. Publ. Math. No. 37 (1969), pp. 27–115.Google Scholar
2. Fine, N. J., Binomial coefficients modulo a prime, Amer. Math. Monthly 54 (1947), pp. 589–592.Google Scholar
3. Haggard, P. W. and Kiltenen, J. O., Binomial expansions modulo prime powers, Internat. J. Math, and Math. Sc. 3 (1980), pp. 397–400.Google Scholar
4. Lucas, E., Théorie des nombres, Tome 1, Librairie Scientifique et Technique Albert Blanchard, Paris (1961) (Original 1891).Google Scholar