Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T07:27:36.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Gelfand Pairs Involving the Wreath Product of Finite Abelian Groups with Symmetric Groups

Part of: Algebraic combinatorics Representation theory of groups

Published online by Cambridge University Press:  13 April 2020

Omar Tout
Omar Tout*
Affiliation:
Department of Mathematics, Faculty of Sciences III, Lebanese University, Tripoli, Lebanon
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that the pair 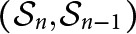$(\mathcal {S}_n,\mathcal {S}_{n-1})$ is a Gelfand pair where 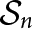$\mathcal {S}_n$ is the symmetric group on n elements. In this paper, we prove that if G is a finite group then 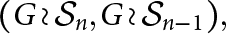$(G\wr \mathcal {S}_n, G\wr \mathcal {S}_{n-1}),$ where 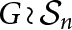$G\wr \mathcal {S}_n$ is the wreath product of G by 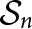$\mathcal {S}_n,$ is a Gelfand pair if and only if G is abelian.

Keywords

Gelfand pairsrepresentation theory of finite groupswreath product of finite abelian groups with symmetric groups

MSC classification

Primary: 05E10: Combinatorial aspects of representation theory
Secondary: 20C30: Representations of finite symmetric groups
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 91 - 97
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aker, K. and Can, M., From parking functions to Gelfand pairs. Proc. Amer. Math. Soc. 140(2012), 1113–1124. https://doi.org/10.1090/S0002-9939-2011-11010-4.CrossRefGoogle Scholar
Brender, M., Spherical functions on the symmetric groups. J. Algebra 42(1976), 302–314. https://doi.org/10.1016/0021-8693(76)90101-0.CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Scarabotti, F., and Tolli, F., Harmonic analysis on finite groups: representation theory, Gelfand pairs and Markov chains. Cambridge Studies in Advanced Mathematics, 108, Cambridge University Press, Cambridge, 2008. https://doi.org/10.1017/CB09780511619823.CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Scarabotti, F., and Tolli, F., Representation theory of the symmetric groups: the Okounkov-Vershik approach, character formulas, and partition algebras. Cambridge Studies in Advanced Mathematics, 121, Cambridge University Press, Cambridge, 2010. https://doi.org/10.1017/CB09781139192361.CrossRefGoogle Scholar
Diaconis, P., Group representations in probability and statistics. Institute of Mathematical Statistics Lecture Notes–Monograph Series, 11, Institute of Mathematical Statistics, Hayward, CA, 1988.Google Scholar
Jack, H., A class of symmetric polynomials with a parameter. Proc. Roy. Soc. Edinburgh Sect. A 69(1970/71), 1–18.Google Scholar
Jack, H., A surface integral and symmetric functions. Proc. Roy. Soc. Edinburgh Sect. A 69(1972), 347–364.Google Scholar
Macdonald, I., Symmetric functions and Hall polynomials. 2nd ed., Oxford Mathematical Monographs, Oxford University Press, New York, 1995.Google Scholar
Sagan, B. E., The symmetric group. Representations, combinatorial algorithms, and symmetric functions. Graduate Texts in Mathematics, 203, Springer-Verlag, New York, 2001.Google Scholar
Stein, I., The Littlewood-Richardson rule for wreath products with symmetric groups and the quiver of the category F\wr FI_{n}. Comm. Algebra 45(2017), 2105–2126. https://doi.org/10.1080/00927872.2016.1226880.CrossRefGoogle Scholar
Strahov, E., Generalized characters of the symmetric group. Adv. Math. 212(2007), 109–142. https://doi.org/10.1016/j.aim.2006.09.017.CrossRefGoogle Scholar
Tout, O., On the symmetric Gelfand pair \left({\mathbf{\mathcal{H}}}_n\times {\mathbf{\mathcal{H}}}_{n-1},\operatorname{diag}\left({\mathbf{\mathcal{H}}}_{n-1}\right)\right). J. Algebra Applic. https://doi.org/10.1142/S0219498821500857.Google Scholar
Tout, O., Structure coefficients of the Hecke algebra of \left({S}_{2n},{B}_n\right). Electron. J. Combin. 21(2014), P4–35.CrossRefGoogle Scholar