Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-02T18:13:56.658Z Has data issue: false hasContentIssue false
  • English
  • Français

A Functional Equation Arising from Ivory's Theorem in Geometry

Published online by Cambridge University Press:  20 November 2018

Hiroshi Haruki
Hiroshi Haruki*
Affiliation:
University of Waterloo, Waterloo OntarioCanada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In previous papers (see [1, 2, 3, 4]), we solved the following functional equation:

1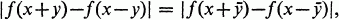

wheref=f(z) is an entire function of a complex variable z and x, y are complex variables.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 4 , October 1975 , pp. 507 - 516
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Haruki, Hiroshi, On Ivory’s Theorem, Mathematica Japonicae, 1 (1949) 151.Google Scholar
2. Haruki, Hiroshi, On the functional equations |f(x+iy)| = |f(x)+f(iy)| and |f(x+iy)| = |f(x) - f(iy)| and on Ivory’s Theorem, Canadian Mathematical Bulletin, 9 (1966) 473–480.Google Scholar
3. Haruki, Hiroshi, On parallelogram functional equations, Mathematische Zeitschrift, 104 (1968) 358–363.Google Scholar
4. Haruki, Hiroshi, On inequalities generalizing a functional equation connected with Ivory’s Theorem, American Mathematical Monthly, 75 (1968) 624–627.Google Scholar
5. Haruki, Hiroshi, An application of Picard’s Theorem to an extension of sine functional equations, Bulletin of the Calcutta Mathematical Society, 62 (1970) 129–132.Google Scholar
6. Zwirner, Kurt, Orthogonalsysteme, in denen Ivorys Theorem gilt, Abhand aus dem Hamburgischen Mathematischen Seminar, 5 (1926–27) 313–336.Google Scholar