Hostname: page-component-6bf8c574d5-pdxrj Total loading time: 0 Render date: 2025-03-07T08:18:17.605Z Has data issue: false hasContentIssue false
  • English
  • Français

From the Ideal Theorem to the class number

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  26 May 2023

Olivier Bordellès Open the ORCID record for Olivier Bordellès [Opens in a new window]
Olivier Bordellès*
Affiliation:
Lycée Dupuy, Le Puy-en-Velay, 2, allée de la Combe, Aiguilhe 43000, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we provide an explicit upper bound for 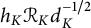$h_K \mathcal {R}_K d_K^{-1/2}$ which depends on an effective constant in the error term of the Ideal Theorem.

Keywords

Class numberDedekind zeta-functionIdeal Theorem

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants 11R42: Zeta functions and $L$-functions of number fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 4 , December 2023 , pp. 1368 - 1375
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayoub, R. G., A mean value theorem for quadratic fields . Pacific J. Math. 8(1958), 23–27.CrossRefGoogle Scholar
Bordellès, O., Arithmetic tales, Advanced Edition, Universitext, Springer, Basel, 2020.CrossRefGoogle Scholar
Chandrasekharan, K. and Narasimhan, R., The approximate functional equation for a class of zeta-functions . Math. Ann. 152(1963), 30–64.CrossRefGoogle Scholar
Gould, H. W., Combinatorial identities. A standardized set of tables listing 500 binomial coefficient summations, Henry E. Gould. VIII, Morgantown, WV, 1972.Google Scholar
Ivić, A., The Riemann zeta-function. Theory and applications, republication of the John Wiler & Sons Ed., Dover, Mineola, NY, 2003.Google Scholar
Lee, E. S., On the number of integral ideals in a number field . J. Math. Anal. Appl. 517(2023), Article ID 126585, 25 pp.CrossRefGoogle Scholar
Louboutin, S., Explicit bounds for residues of Dedekind zeta functions, values of $L$ -functions at $s=1$ , and relative class numbers . J. Number Theory 85(2000), 263–282.CrossRefGoogle Scholar
Louboutin, S., Explicit upper bounds for residues of Dedekind zeta functions and values of $L$ -functions at $s=1$ , and explicit lower bounds for relative class numbers of $CM$ -fields . Canad. J. Math. 53(2001), 1194–1222.CrossRefGoogle Scholar
Stas, W., On the order of the Dedekind zeta-function near the line $\sigma =1$ . Acta Arith. 35(1979), 195—202.CrossRefGoogle Scholar
Sunley, J. E., On the class numbers of totally imaginary quadratic extensions of totally real fields. Ph.D. thesis, University of Maryland, College Park, MD, 1971.CrossRefGoogle Scholar
Tenenbaum, G., Introduction à la Théorie Analytique et Probabiliste des Nombres, Belin, 2008 (French).Google Scholar
Titchmarsh, E. M., The theory of the Riemann zeta-function, Clarendon Press, Oxford, 1986. Notes by Heath-Brown, D. R..Google Scholar
Lee, E. S., On the number of ideals in a number fields, preprint, 23 pp., 2022.Google Scholar