Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-18T14:14:18.112Z Has data issue: false hasContentIssue false
  • English
  • Français

From Matrix to Operator Inequalities

Published online by Cambridge University Press:  20 November 2018

Terry A. Loring
Terry A. Loring*
Affiliation:
Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, U.S.A.e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We generalize Löwner's method for proving that matrix monotone functions are operator monotone. The relation 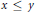$x\,\le \,y$ on bounded operators is our model for a definition of 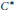${{C}^{*}}$-relations being residually finite dimensional.

Our main result is a meta-theorem about theorems involving relations on bounded operators. If we can show there are residually finite dimensional relations involved and verify a technical condition, then such a theorem will follow from its restriction to matrices.

Applications are shown regarding norms of exponentials, the norms of commutators, and “positive” noncommutative $*$-polynomials.

Keywords

46L0547B99C*-algebrasmatricesbounded operatorsrelationsoperator normordercommutatorexponentialresidually finite dimensional
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 339 - 350
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Archbold, R. J., On residually finite-dimensional C*-algebras. Proc. Amer. Math. Soc. 123(1995), no. 9, 2935–2937.Google Scholar
[2] Bendat, J. and Sherman, S., Monotone and convex operator functions. Trans. Amer. Math. Soc. 79(1955), 58–71.Google Scholar
[3] Bhatia, R., Matrix analysis. Graduate Texts in Mathematics, 169, Springer-Verlag, New York, 1997.Google Scholar
[4] Bhatia, R. and Kittaneh, F., Some inequalities for norms of commutators. SIAM J. Matrix Anal. Appl. 18(1997), no. 1, 258–263. http://dx.doi.org/10.1137/S0895479895293235 Google Scholar
[5] Blackadar, B., Operator algebras. Theory of C*-algebras and von Neumann algebras. Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-commutative Geometry, III. Springer-Verlag, Berlin, 2006.Google Scholar
[6] Blackadar, B., Shape theory for C*-algebras. Math. Scand. 56(1985), no. 2, 249–275.Google Scholar
[7] Dixmier, J., C*-algebras. North-Holland Mathematical Library, 15, North-Holland Publishing Co., Amsterdam-New York-Oxford, 1977.Google Scholar
[8] Eilers, S. and Exel, R., Finite-dimensional representations of the soft torus. Proc. Amer. Math. Soc. 130(2002), no. 3, 727–731. http://dx.doi.org/10.1090/S0002-9939-01-06150-0 Google Scholar
[9] Exel, R. and Loring, T. A., Finite-dimensional representations of free product C*-algebras. Internat. J. Math. 3(1992), no. 4, 469–476. http://dx.doi.org/10.1142/S0129167X92000217 Google Scholar
[10] Goodearl, K. R. and Menal, P., Free and residually finite-dimensional C*-algebras. J. Funct. Anal. 90(1990), no. 2, 391–410. http://dx.doi.org/10.1016/0022-1236(90)90089-4 Google Scholar
[11] Hadwin, D., Kaonga, L., and Mathes, B., Noncommutative continuous functions. J. Korean Math. Soc. 40(2003), no. 5, 789–830. http://dx.doi.org/10.4134/JKMS.2003.40.5.789 Google Scholar
[12] Helton, J. W., “Positive” noncommutative polynomials are sums of squares. Ann. of Math. (2) 156(2002), no. 2, 675–694. http://dx.doi.org/10.2307/3597203 Google Scholar
[13] Loring, T. A., C*-algebra relations. Math. Scand. 107(2010), no. 1, 43–72.Google Scholar
[14] McCullough, S. and Putinar, M., Noncommutative sums of squares. Pacific J. Math. 218(2005), no. 1, 167–171. http://dx.doi.org/10.2140/pjm.2005.218.167 Google Scholar
[15] Pedersen, G. K., C*-algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press Inc., London-New York, 1979.Google Scholar
[16] Pedersen, G. K., A commutator inequality. In: Operator algebras, mathematical physics, and low-dimensional topology (Istanbul, 1991), Res. Notes Math., 5, A K Peters, Wellesley, MA, 1993, pp. 233–235.Google Scholar
[17] Phillips, N. C., Inverse limits of C*-algebras and applications. In: Operator algebras and applications, Vol. 1, London Math. Soc. Lecture Note Ser., 135, Cambridge University Press, Cambridge, 1988, pp. 127–185.Google Scholar