No CrossRef data available.
Article contents
Footnote to a Formula of Gioia and Subbarao
Published online by Cambridge University Press: 20 November 2018
Extract
Recently Gioia and Subbarao [2] studied essentially the following problem: If g(n) is an arithmetic function, and 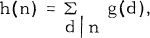 , then what is the behaviour of H(a, n) defined for each fixed integer a ≥ 2 by
, then what is the behaviour of H(a, n) defined for each fixed integer a ≥ 2 by
1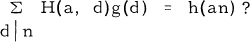
By using Vaidyanathaswamy′s formula [e.g., 1], they obtain an explicit formula for H(a, n) in case g(n) is positive and completely multiplicative (Formula 2.2 of [2]). However, Vaidyanathaswamy′s formula is unnecessary to the proof of this result, which indeed follows more simply without its use, by exploiting a simple idea used earlier by Subbarao [3] (referred to also in the course of [2]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1967


