Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T02:10:43.469Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fixed Point Set of Real Multi-Valued Contraction Mappings

Published online by Cambridge University Press:  20 November 2018

Arthur S. Finbow
Arthur S. Finbow*
Affiliation:
Dalhousie University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, d1) and (Y, d2) be metric spaces. A mapping f:X→Y is said to be a Lipschitz mapping if there exists a real number λ such that

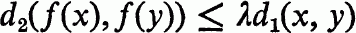
for each x,y∊X. We call λ a Lipschitz constant for f. If λ∊[0, 1), f is called a contraction mapping. Throughout this note CB(Y) denotes the set of closed and bounded subsets of Y equipped with the Hausdorff metric induced by d2.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 4 , December 1972 , pp. 507 - 511
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Nadler, S. B. Jr, Multi-valued contraction mappings, Pacific J. Math. 30 (1969), 475-488.Google Scholar
2. Helga, Schirmer, Properties of the fixed point set of contractive multi-functions, Canad. Math. Bull. 13 (1970), 169-173.Google Scholar