Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-07T23:07:41.977Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fixed Point Locus of the Verschiebung on ℳX(2, 0) for Genus-2 Curves X in Charateristic 2

Published online by Cambridge University Press:  20 November 2018

YanHong Yang
YanHong Yang*
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for every ordinary genus-2 curve 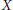$X$ over a finite field $\kappa$ of characteristic 2 with 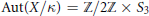$\text{Aut}\left( X/\kappa \right)\,=\,\mathbb{Z}/2\mathbb{Z}\,\times \,{{S}_{3}}$ there exist 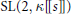$\text{SL}\left( 2,\,\kappa \left[\!\left[ s \right]\!\right] \right)$-representations of 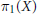${{\pi }_{1}}\left( X \right)$ such that the image of 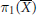${{\pi }_{1}}\left( \overline{X} \right)$ is infinite. This result produces a family of examples similar to Y. Laszlo’s counterexample to A. J. de Jong’s question regarding the finiteness of the geometric monodromy of representations of the fundamental group.

Keywords

14H6014D0514G15vector bundleFrobenius pullbackrepresentationetale fundamental group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 439 - 448
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Ancochea, G., Corps hyperelliptiques abstraits de caractéristique deux. Portugaliae Math. 4 (1943, 119–128.Google Scholar
[2] Biswas, I. and Ducrohet, L., An analog of a theorem of Lange and Stuhler for principal bundles. C. R. Math. Acad. Sci. Paris 345 (2007, no. 9, 495–497 http://dx.doi.org/10.1016/j.crma.2007.10.010 Google Scholar
[3] Böckle, G. and Khare, C., Mod l representations of arithmetic fundamental groups. II. A conjecture of A. J. de Jong. Compos. Math. 142 (2006, no. 2, 271–294.http://dx.doi.org/10.1112/S0010437X05002022 CrossRefGoogle Scholar
[4] Esnault, H. and Langer, A., On a positive equicharacteristic variant of the p-curvature conjecture. arxiv:1108.0103Google Scholar
[5] Freitag, E. and Kiehl, R., ´ Etale cohomology and the Weil conjecture. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 13, Springer-Verlag, Berlin, 1988.Google Scholar
[6] Gaitsgory, D., On de Jong's conjecture. Israel J. Math. 157 (2007, 155–191.http://dx.doi.org/10.1007/s11856-006-0006-2 Google Scholar
[7] Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves. Second ed., Cambridge Mathematical Library, Cambridge University Press, Cambridge, 2010.Google Scholar
[8] Isaacs, I. M., Character theory of finite groups. Pure and Applied Mathematics, 69, Academic Press, New York-London, 1976.Google Scholar
[9] Jong, A. J. de, A conjecture on arithmetic fundamental groups. Israel J. Math. 121 (2001, 61–84.http://dx.doi.org/10.1007/BF02802496 CrossRefGoogle Scholar
[10] Lange, H. and Pauly, C., On Frobenius-destabilized rank-2 vector bundles over curves. Comment. Math. Helv. 83 (2008, no. 1, 179–209.http://dx.doi.org/10.4171/CMH/122 Google Scholar
[11] Lange, H. and Stuhler, U., Vektorb¨undel auf Kurven und Darstellungen der algebraischen Fundamentalgruppe. Math. Z. 156 (1977, no. 1, 73–83.http://dx.doi.org/10.1007/BF01215129 CrossRefGoogle Scholar
[12] Laszlo, Y., A non-trivial family of bundles fixed by the square of Frobenius. C. R. Math. Acad. Sci. Paris Sér. I Math. 333 (2001, no. 7, 651–656.http://dx.doi.org/10.1016/S0764-4442(01)02109-7 Google Scholar
[13] Laszlo, Y. and Pauly, C., The action of the Frobenius map on rank 2 vector bundles in characteristic 2. J. Algebraic Geom. 11 (2002, no. 2, 219–243.http://dx.doi.org/10.1090/S1056-3911-01-00310-1 CrossRefGoogle Scholar
[14] Laszlo, Y., The Frobenius map, rank 2 vector bundles and Kummer's quartic surface in characteristic 2 and 3. Adv. Math. 185 (2004, no. 2, 246–269.http://dx.doi.org/10.1016/S0001-8708(03)00211-1 Google Scholar
[15] Milne, J. S., ´ Etale cohomology. Princeton Mathematical Series, 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[16] Mumford, D., Abelian varieties. Tata Institute of Fundamental Research in Mathematics, 5, Hindustan Book Agency, New Delhi, 2008.Google Scholar
[17] Raynaud, M., Sections des fibrés vectoriels sur une courbe. Bull. Soc. Math. France 110 (1982, no. 1, 103–125.Google Scholar