Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T16:23:20.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Faltings' Finiteness Dimension of Local Cohomology Modules Over Local Cohen–Macaulay Rings

Published online by Cambridge University Press:  20 November 2018

Kamal Bahmanpour  and
Reza Naghipour
Kamal Bahmanpour
Affiliation:
Department of Mathematics, Faculty of Sciences, University of Mohaghegh Ardabili, 56199-11367, Ardabil, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), 19395-5746, Tehran, Iran. e-mail: [email protected]
Reza Naghipour
Affiliation:
Department of Mathematics, University of Tabriz, Tabriz, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), 19395-5746, Tehran, Iran. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 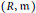$(R,\mathfrak{m})$ denote a local Cohen–Macaulay ring and $I$ a non-nilpotent ideal of $R$. The purpose of this article is to investigate Faltings’ finiteness dimension 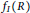${{f}_{I}}(R)$ and the equidimensionalness of certain homomorphic images of $R$. As a consequence we deduce that 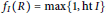${{f}_{I}}(R)=\max \{1,\text{ht}I\}$, and if 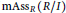$\text{mAs}{{\text{s}}_{R}}(R/I)$ is contained in 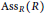$\text{As}{{\text{s}}_{R}}(R)$, then the ring 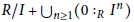$R/I+{{\bigcup }_{n\ge 1}}(0{{:}_{R}}{{I}^{n}})$ is equidimensional of dimension dim 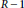$R-1$. Moreover, we will obtain a lower bound for injective dimension of the local cohomology module 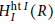$H_{I}^{\text{ht}I}(R)$, in the case where 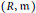$(R,\mathfrak{m})$ is a complete equidimensional local ring.

Keywords

13D4514B15Cohen Macaulay ringequidimensional ringfiniteness dimensionlocal cohomology
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 2 , 01 June 2017 , pp. 225 - 234
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bagheriyeh, I., A'zami, J., and Bahmanpour, K., Generalization of the Lichtenbaum-Hartshorne vanishing theorem. Comm. Algebra 40(2012), 134–137. http://dx.doi.org/10.1080/00927872.2010.525225 Google Scholar
[2] Bahmanpour, K. and Naghipour, R., Cofiniteness of local cohomology modules for ideals of small dimension. J. Algebra 321(2009), 1997–2011. http://dx.doi.org/10.1016/j.jalgebra.2008.12.020 Google Scholar
[3] Brodmann, M. P. and Sharp, R. Y., Local cohomology: an algebraic introduction with geometric applications. Cambridge University Press, Cambridge, 1998. http://dx.doi.org/1 0.101 7/CBO9780511 629204 Google Scholar
[4] Bruns, W. and Herzog, J., Cohen-Macaulay rings. Cambridge Studies in Advanced Mathematics, 39, Cambridge Univeristy Press, Cambridge, UK, 1998. Google Scholar
[5] Divaani-Aazar, K., Naghipour, R. and Tousi, M. Cohomological dimension of certain algebraic varieties. Proc. Amer. Math. Soc. 130(2002), 3537–3544. http://dx.doi.org/1 0.1090/S0002-9939-02-06500-0 Google Scholar
[6] Hartshorne, R., Local cohomology: A seminar given by A. Grothendieck, Harvard University, Fall, 1961. Lecture Notes in Mathematics, 862, Springer-Verlag, Berlin-New York, 1967. Google Scholar
[7] Hartshorne, R. and Speiser, R., Local cohomological dimension in characteristic p. Ann. of Math. 105(1977), 45–79. http://dx.doi.org/10.2307/1971025 Google Scholar
[8] Huneke, C. and Sharp, R. Y., Bass numbers of local cohomology modules. Trans. Amer. Math. Soc. 339(1993), 765–779. http://dx.doi.org/10.1090/S0002-9947-1993-1124167-6 Google Scholar
[9] Lyubeznik, G., Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra). Invent. Math. 113(1993), 41–55. http://dx.doi.org/10.1007/BF01244301 Google Scholar
[10] Man, A., Some results on local cohomology modules. Arch. Math. (Basel) 87(2006), 211–216. http://dx.doi.org/10.1007/s00013-006-1674-1 Google Scholar
[11] Marley, T. and Vassilev, J. C., Cofiniteness and associated primes of local cohomology modules. J. Algebra 256(2002), 180–193. http://dx.doi.org/10.1016/SOO21-8693(02)00151-5 Google Scholar
[12] Matsumura, H., Commutative ring theory. Cambridge Studies in Advanced Mathematics, 8, Cambridge University Press, Cambridge, 1986. Google Scholar
[13] Melkersson, L., Modules cofinite with respect to an ideal. J. Algebra 285(2005), 649–668. http://dx.doi.org/10.1016/j.jalgebra.2004.08.037 Google Scholar
[14] Schenzel, P., Proregular sequences, local cohomology and completion. Math. Scand. 92(2003), 161–180. http://dx.doi.org/10.7146/math.scand.a-14399 Google Scholar