Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T09:48:38.131Z Has data issue: false hasContentIssue false
  • English
  • Français

Factorization into Symmetries and Transvections of Given Conjugacy Classes

Published online by Cambridge University Press:  20 November 2018

Frieder Knüppel
Frieder Knüppel*
Affiliation:
Mathematisches Seminar Universität Kiel Olshausenstraβe 40 23 Kiel Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The u-invariant u(K) of a field K is the smallest number 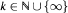such that every k-dimensional regular quadratic form over K is universal. Let O(V,f) be the orthogonal group of a finite-dimensional regular metric vector space over a field K of characteristic distinct from 2. Let π ∊ 0(V), B(π) := V(π - 1), dim[B(π) ∩ kernel(π - 1)] > u(K). Given λ1,..., λm ∊ K* where m := dim B(π) - u(K) + 1. Then π = σ1······σk where k := dim B(π) and σi is a symmetry with negative space Kai and f(ai, ai) = λi for i ∊ { 1 , . . . , m}. We prove similar theorems also for symplectic groups where transvections are taken as generators.

Keywords

51N3011E5715A2314L35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 400 - 409
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Ellers, E. W. and Malzan, J., Products of Reflections in the Kernel of the Spinorial Norm, Geom. Ded. 36(1990), 279–285. 2 , Products of X-Transvections in Sp(2n, q), Linear Algebra and Appl. 146(1991), 121–132.Google Scholar
3. Hahn, J. and O'Meara, O. T., The Classical Groups and K-Theory , Springer, 1989.Google Scholar
4. Wall, G. E., On the Conjugacy Classes in the Unitary, Symplectic and Orthogonal Groups, J. Austral. Math. Soc. 111(1963), 1–62.Google Scholar