Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Farenick, Douglas
1996.
Irreducible positive linear maps on operator algebras.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 11,
p.
3381.
El Kadiri, Mohamed
1998.
Opérateurs positifs sur certains espaces de formes quadratiques.
Linear Algebra and its Applications,
Vol. 283,
Issue. 1-3,
p.
273.
Ha, Kil-Chan
Kye, Seung-Hyeok
and
Park, Young Sung
2003.
Entangled states with positive partial transposes arising from indecomposable positive linear maps.
Physics Letters A,
Vol. 313,
Issue. 3,
p.
163.
Kye, Seung-Hyeok
2003.
Facial structures for unital positive linear maps in the two-dimensional matrix algebra.
Linear Algebra and its Applications,
Vol. 362,
Issue. ,
p.
57.
Życzkowski, Karol
and
Bengtsson, Ingemar
2004.
On Duality between Quantum Maps and Quantum States.
Open Systems & Information Dynamics,
Vol. 11,
Issue. 01,
p.
3.
Kye, Seung-Hyeok
2005.
Facial Structures for Decomposable Positive Linear Maps in Matrix Algebras.
Positivity,
Vol. 9,
Issue. 1,
p.
57.
Majewski, W.A.
2007.
On positive decomposable maps.
Reports on Mathematical Physics,
Vol. 59,
Issue. 3,
p.
289.
Ha, Kil-Chan
and
Kye, Seung-Hyeok
2011.
Entanglement Witnesses Arising from Exposed Positive Linear Maps.
Open Systems & Information Dynamics,
Vol. 18,
Issue. 04,
p.
323.
Ha, Kil-Chan
and
Kye, Seung-Hyeok
2012.
Optimality for indecomposable entanglement witnesses.
Physical Review A,
Vol. 86,
Issue. 3,
Kye, Seung-Hyeok
2012.
Necessary Conditions for Optimality of Decomposable Entanglement Witnesses.
Reports on Mathematical Physics,
Vol. 69,
Issue. 3,
p.
419.
Klimas, Andrew J.
and
Hill, Richard D.
2012.
On the Completely Positive and Positive Semidefinite-Preserving Cones—Part III.
ISRN Algebra,
Vol. 2012,
Issue. ,
p.
1.
Chruściński, Dariusz
and
Sarbicki, Gniewomir
2012.
Exposed positive maps: a sufficient condition.
Journal of Physics A: Mathematical and Theoretical,
Vol. 45,
Issue. 11,
p.
115304.
Ha, Kil-Chan
and
Kye, Seung-Hyeok
2012.
Geometry of the Faces for Separable States Arising from Generalized Choi Maps.
Open Systems & Information Dynamics,
Vol. 19,
Issue. 02,
p.
1250009.
KYE, SEUNG-HYEOK
2013.
FACIAL STRUCTURES FOR VARIOUS NOTIONS OF POSITIVITY AND APPLICATIONS TO THE THEORY OF ENTANGLEMENT.
Reviews in Mathematical Physics,
Vol. 25,
Issue. 02,
p.
1330002.
Majewski, Władysław A.
and
Tylec, Tomasz I.
2013.
On the structure of positive maps. II. Low dimensional matrix algebras.
Journal of Mathematical Physics,
Vol. 54,
Issue. 7,
Sarbicki, Gniewomir
and
Chruściński, Dariusz
2013.
A class of exposed indecomposable positive maps.
Journal of Physics A: Mathematical and Theoretical,
Vol. 46,
Issue. 1,
p.
015306.
Shultz, Fred
2016.
The structural physical approximation conjecture.
Journal of Mathematical Physics,
Vol. 57,
Issue. 1,
Rahaman, Mizanur
2020.
A New Bound on Quantum Wielandt Inequality.
IEEE Transactions on Information Theory,
Vol. 66,
Issue. 1,
p.
147.
Han, Kyung Hoon
Kye, Seung-Hyeok
and
Szalay, Szilárd
2020.
Partial separability/entanglement violates distributive rules.
Quantum Information Processing,
Vol. 19,
Issue. 7,


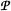 denote the convex set of all positive linear maps from the matrix algebra
denote the convex set of all positive linear maps from the matrix algebra 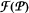 of all faces of
of all faces of 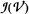 of all join homomorphisms between the lattice
of all join homomorphisms between the lattice 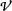 of all subspaces of ℂ
of all subspaces of ℂ