Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-30T19:33:56.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Extrapolation of Lp Data from a Modular Inequality

Published online by Cambridge University Press:  20 November 2018

Steven Bloom  and
Ron Kerman
Steven Bloom
Affiliation:
Siena College, Loudonville, NY 12211, USA
Ron Kerman
Affiliation:
Brock University, St. Catharines, Ontario, L2S 3A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If an operator 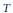$T$ satisfies a modular inequality on a rearrangement invariant space 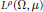${{L}^{\rho}}\left( \Omega ,\mu \right)$, and if 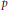$p$ is strictly between the indices of the space, then the Lebesgue inequality 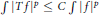$\int{|Tf{{|}^{P}}\le C\int{|f{{|}^{P}}}}$ holds. This extrapolation result is a partial converse to the usual interpolation results. A modular inequality for Orlicz spaces takes the form 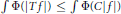$\int{\Phi \left( |Tf| \right)\le }\int{\Phi \left( C|f| \right)}$, and here, one can extrapolate to the (finite) indices 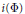$i\left( \Phi \right)$ and $I\left( \Phi \right)$ as well.

Keywords

42B25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 1 , 01 March 2002 , pp. 25 - 35
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Bennett, C. and Sharpley, R., Interpolation of Operators. Academic Press, Orlando, 1988.Google Scholar
[2] Bloom, S. and Kerman, R., Weighted LΦ integral inequalities for operators of Hardy type. Studia Math. 110 (1994), 35–52.Google Scholar
[3] Boyd, D. W., Indices for the Orlicz spaces. Pacific J. Math. 38 (1971), 315–323.Google Scholar
[4] Kokilashvili, V. and Krbec, M., Weighted Inequalities in Lorentz and Orlicz Spaces. World Scientific, 1991.Google Scholar
[5] Krasnosel’skii, M. A. and Rutickii, Ya. B., Convex Functions and Orlicz Spaces (translation). P. Noordhoff Ltd., Groningen, 1961.Google Scholar
[6] Lindenstrauss, J. and Tzafiri, L., Classical Banach Spaces I and II. Springer-Verlag, Berlin-Heidelberg-New York, 1977 and 1979.Google Scholar
[7] Maligranda, L., Indices and interpolation. Dissert. Math. 234 (1985), 1–49.Google Scholar
[8] Matuszewska, W. and Orlicz, W., On certain properties of ϕ-functions. Bull. Acad. Polon. Sci., Ser. Sci. Math. Astr. et Phys. 8 (1960), 439–443.Google Scholar
[9] Musielak, J., Orlicz Spaces and Modular Spaces. Lecture Notes in Mathematics 1034, Springer-Verlag, Berlin-Heidelberg-New York-Tokyo, 1983.Google Scholar
[10] Rao, M. M. and Ren, Z. D., Theory of Orlicz Spaces. Marcel Dekker, Inc., New York, 1991.Google Scholar
[11] Shimogaki, T., A note on norms of compression operators on function spaces. Proc. Japan Acad. 46 (1970), 239–242.Google Scholar
[12] Stein, E. M. and Weiss, G. W., An extension of a theorem of Marcinkiewicz and some of its applications. J. Math. Mech. 8 (1959), 263–284.Google Scholar