Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T06:20:59.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of Some Theorems of W. Schwarz

Published online by Cambridge University Press:  20 November 2018

Michael Coons
Michael Coons*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON N2L 3G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove that a non–zero power series 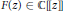$F(z\text{)}\in \mathbb{C}\text{ }[[z]]$ satisfying

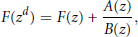$$F({{z}^{d}})\,=\,F(z)\,+\,\frac{A(z)}{B(z)},$$

where 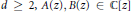$d\,\ge \,2,\,A(z),\,B(z)\,\in \,\mathbb{C}[z]$, with 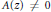$A(z)\,\ne \,0$ and 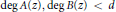$\deg \,A(z),\,\deg \,B(z)\,<\,d$ is transcendental over 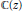$\mathbb{C}(z)$. Using this result and a theorem of Mahler’s, we extend results of Golomb and Schwarz on transcendental values of certain power series. In particular, we prove that for all 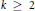$k\,\ge \,2$ the series 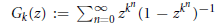${{G}_{k}}(z):=\mathop{\sum }_{n=0}^{\infty }{{z}^{{{k}^{n}}}}{{(1-{{z}^{{{k}^{n}}}})}^{-1}}$ is transcendental for all algebraic numbers $z$ with 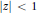$\left| z \right|\,<\,1$. We give a similar result for 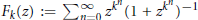${{F}_{k}}(z):=\mathop{\sum }_{n=0}^{\infty }{{z}^{{{k}^{n}}}}{{(1+{{z}^{{{k}^{n}}}})}^{-1}}$. These results were known to Mahler, though our proofs of the function transcendence are new and elementary; no linear algebra or differential calculus is used.

Keywords

11B3711J81functional equationstranscendencepower series
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 60 - 66
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Duverney, D., Transcendence of a fast converging series of rational numbers. Math. Proc. Cambridge Philos. Soc. 130(2001), no. 2, 193–207. doi:10.1017/S0305004100004783Google Scholar
[2] Duverney, D. and Nishioka, K., An inductive method for proving the transcendence of certain series. Acta Arith. 110(2003), no. 4, 305–330. doi:10.4064/aa110-4-1Google Scholar
[3] Duverney, D., Kanoko, T., and Tanaka, T., Transcendence of certain reciprocal sums of linear recurrences. Monatsh. Math. 137(2002), no. 2, 115–128. doi:10.1007/s00605-002-0501-4Google Scholar
[4] Golomb, S. W., On the sum of the reciprocals of the Fermat numbers and related irrationalities. Canad. J. Math. 15(1963), 475–478. doi:10.4153/CJM-1963-051-0Google Scholar
[5] Mahler, K., Arithmetische Eigenschaften der Lösungen einer Klasse von Funktionalgleichungen. Math. Ann. 101(1929), no. 1, 342–366. doi:10.1007/BF01454845Google Scholar
[6] Mahler, K., Arithmetische Eigenschaften einer Klasse transzendental- transzendenter Funktionen. Math. Z. 32(1930), 545–585. doi:10.1007/BF01194652Google Scholar
[7] Mahler, K., Über das Verschwinden von Potenzreihen mehrerer Ver änderlicher in speziellen Punktfolgen. Math. Ann. 103(1930), no. 1, 573–587. doi:10.1007/BF01455711Google Scholar
[8] Mahler, K., Remarks on a paper by W. Schwarz. J. Number Theory 1(1969), 512–521. doi:10.1016/0022-314X(69)90013-4Google Scholar
[9] Nishioka, Keiji, Algebraic function solutions of a certain class of functional equations. Arch. Math. 44(1985), no. 4, 330–335.Google Scholar
[10] Nishioka, Kumiko, Mahler Functions and Transcendence. Lecture Notes in Mathematics, 1631, Springer-Verlag, Berlin, 1996.Google Scholar
[11] Schwarz, W., Remarks on the irrationality and transcendence of certain series. Math. Scand 20(1967), 269–274.Google Scholar