Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T08:59:01.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of Maps to Nilpotent Spaces

Published online by Cambridge University Press:  20 November 2018

M. Cencelj  and
A. N. Dranishnikov
M. Cencelj
Affiliation:
IMFM University of Ljubljana P. O. B. 2964 SI-1001 Ljubljana Slovenia, e-mail: [email protected]
A. N. Dranishnikov
Affiliation:
Pennsylvania State University Mathematics Department 218 McAllister Building University Park, Pennsylvania 16802 U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that every compactum has cohomological dimension 1 with respect to a finitely generated nilpotent group 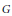$G$ whenever it has cohomological dimension 1 with respect to the abelianization of 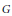$G$. This is applied to the extension theory to obtain a cohomological dimension theory condition for a finite-dimensional compactum 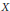$X$ for extendability of every map from a closed subset of 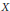$X$ into a nilpotent 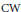$\text{CW}$-complex 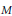$M$ with finitely generated homotopy groups over all of 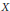$X$.

Keywords

55M1055S3654C2054F45cohomological dimensionextension of mapsnilpotent groupnilpotent space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 266 - 269
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Dranishnikov, A. N., Extension of mappings into CW-complexes. Mat. Sb. (9) 182 (1991), 1300–1310; in English, Math. USSR-Sb. (1) 74 (1993), 47–56.Google Scholar
[2] Dold, Albrecht and Thom, René, Quasifaserungen und unendliche symmetrische Produkte. Ann. of Math. (2) 67 (1958), 239–281.Google Scholar
[3] Hilton, Peter, Homotopy theory and duality. Gordon and Breach, New York, 1965.Google Scholar
[4] Hilton, Peter, Mislin, Guido and Roitberg, Joseph, Localization of Nilpotent Groups and Spaces. North-Holland, Amsterdam, 1975.Google Scholar