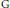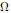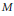Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baracco, Luca
and
Pinton, Stefano
2013.
Propagation of CR extendibility at the vertex of a complex sector.
Mathematische Nachrichten,
Vol. 286,
Issue. 2-3,
p.
109.
Baracco, Luca
Fassina, Martino
and
Pinton, Stefano
2020.
An extension theorem for regular functions of two quaternionic variables.
Journal of Mathematical Analysis and Applications,
Vol. 482,
Issue. 2,
p.
123573.
Baracco, Luca
and
Pinton, Stefano
2022.
Higher Order Gradients of Monogenic Functions.
The Journal of Geometric Analysis,
Vol. 32,
Issue. 1,