Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T11:20:46.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of a Tight Set Function with Values in a Locally Convex Space

Published online by Cambridge University Press:  20 November 2018

Pedro Morales
Pedro Morales*
Affiliation:
Université de Montréal, Département de Mathématiques, Montréal, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of the paper is to extend a tight set function on a lattice 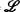with values in a locally convex space of special type to a measure on the cr-ring generated by 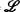. This result generalizes the extension theorem of Thomas [12, p. 151], which in turn contains the extension theorems of Pauc [9, p. 710], Fox [4, p. 525] and J. J. Uhl, Jr. [14, Corollary 2].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 5 , 01 December 1975 , pp. 699 - 702
Copyright
Copyright © Canadian Mathematical Society 1975

References

l. Bessaga, C. and Pelczynski, A., On bases and unconditional convergence of series in Banach spaces, Studia Math. 17 (1958), 151–164.Google Scholar
2. Diestel, J., Applications of weak compactness and bases to vector measures and vectorial integration, Rev. Roumaine Math. Pures Appl. 18 (1973), 211–224.Google Scholar
3. Dinculeanu, N., Vector measures, Pergamon Press, London, New York, 1967.Google Scholar
4. Fox, G., Extension of a bounded vector measure with values in a reflexive Banach space, Canad. Math. Bull. 10 (1967), 525–529.Google Scholar
5. G. G. Gould, Extensions of vector-valued measures, Proc. London Math. Soc. 16 (1966), 685–704.Google Scholar
6. Kluvanek, I., The extension and closure of vector measure, Procedings of the Conference on Vector and Operator-valued Measures, Snowbird, Utah, Academic Press (1973), 168–183.Google Scholar
7. Lipecki, Z., Extensions of tight set functions with values in a topological group, Bull. Acad. Polon. Sci. 22 (1974), 105–113.Google Scholar
8. Métivier, M., Sur les mesures à valeurs vectorielles et les limitesprojectives de telles mesures, C. R. Acad. Se. Paris 256 (1963), 2993–2995.Google Scholar
9. Pauc, C., Prolongement d’une mesure vectorielle jordanienne en une mesure lebesguienne, R. C. Acad. Se. Paris 233 (1946), 709–711.Google Scholar
10. Pettis, B. J., On the extension of measures, Ann. of Math. 54 (1951), 186–197.Google Scholar
11. Rickart, C. E., Decomposition of additive set functions, Duke Math. J. 10 (1943), 653–665.Google Scholar
12. Thomas, G. E., L’intégration par rapport à une mesure de Radon vectorielle, Ann. Inst. Fourier (Grenoble) 20 (1970), 55–191.Google Scholar
13. Tumarkin, Ju. B., On locally convex spaces with bases, Dokl. Akad. Nauk SSSR. 195 (1970), 1278–1281 = Soviet Math. Dokl. 11 (1970), 1672–1675.Google Scholar
14. Uhl, J. J. Jr, Extensions and decompositions of vector measures, J. London Math. Soc. 3 (1971), 672–675.Google Scholar