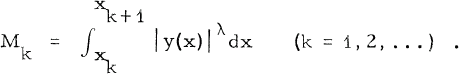Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Muldoon, M. E.
1977.
Higher monotonicity properties of certain Sturm-Liouville functions. V.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 77,
Issue. 1-2,
p.
23.
Muldoon, Martin E.
2008.
Continuous ranking of zeros of special functions.
Journal of Mathematical Analysis and Applications,
Vol. 343,
Issue. 1,
p.
436.


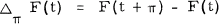 are increasing sequences of consecutive zeros of non-trivial solutions y(x),
are increasing sequences of consecutive zeros of non-trivial solutions y(x), 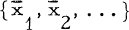 , of the differential equation
, of the differential equation