Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T09:21:52.038Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of Multiple Solutions for a p-Laplacian System in ℝ N with Sign-changing Weight Functions

Published online by Cambridge University Press:  20 November 2018

Hongxue Song ,
Caisheng Chen  and
Qinglun Yan
Hongxue Song
Affiliation:
(Song, Chen) College of Science, Hohai University, Nanjing 210098, P. R. China e-mail: [email protected]
Caisheng Chen
Affiliation:
(Song, Chen) College of Science, Hohai University, Nanjing 210098, P. R. China e-mail: [email protected]
Qinglun Yan
Affiliation:
(Song, Yan) College of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, P. R. China e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the quasi-linear elliptic problem

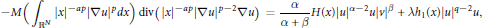$$-M\left( {{\int }_{{{\mathbb{R}}^{N}}}}{{\left| x \right|}^{-ap}}{{\left| {{\nabla }_{u}} \right|}^{p}}dx \right)\,\text{div}\left( {{\left| x \right|}^{-ap}}{{\left| \nabla u \right|}^{p-2}}\nabla u \right)=\frac{\alpha }{\alpha +\beta }H\left( x \right){{\left| u \right|}^{\alpha -2}}u{{\left| v \right|}^{\beta }}+\text{ }\lambda \text{ }{{\text{h}}_{1}}\left( x \right){{\left| u \right|}^{q-2}}u,$$

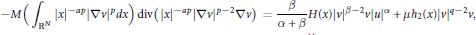$$-M\left( {{\int }_{{{\mathbb{R}}^{N}}}}{{\left| x \right|}^{-ap}}{{\left| \nabla v \right|}^{p}}dx \right)\,\text{div}\left( {{\left| x \right|}^{-ap}}{{\left| \nabla v \right|}^{p-2}}\nabla v \right)=\frac{\beta }{\alpha +\beta }H\left( x \right){{\left| v \right|}^{\beta -2}}v{{\left| u \right|}^{\alpha }}+\mu {{h}_{2}}\left( x \right){{\left| v \right|}^{q-2}}v,$$

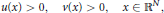$$u\left( x \right)>0,v\left( x \right)>0,x\in {{\mathbb{R}}^{N}},$$

where 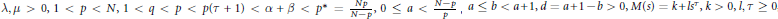$\text{ }\lambda \text{ ,}\mu >\text{0,}\text{1}<\text{p}<\text{N,}\text{1}<\text{q}<\text{p}<\text{p}\left( \tau +1 \right)<\alpha +\beta <{{p}^{*}}=\frac{{{N}_{p}}}{N-p},0\le a<\frac{N-p}{p},a\le b<a+1,d=a+1-b>0,M\left( s \right)=k+l{{s}^{\tau }},k>0,l,\tau \ge 0$ and the weight 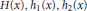$H\left( x \right),\,{{h}_{1}}\left( x \right),\,{{h}_{2}}\left( x \right)$ are continuous functions that change sign in 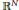${{\mathbb{R}}^{N}}$ . We will prove that the problem has at least two positive solutions by using the Nehari manifold and the fibering maps associated with the Euler functional for this problem.

Keywords

35J66Nehari manifoldquasilinear elliptic systemp-Laplacian operatorconcave and convex nonlinearities
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 417 - 434
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Ambrosetti, A., Brezis, H., and Cerami, G., Combined effects of concave and convex nonlinearities in some elliptic problems. J. Funct. Anal. 122(1994), no. 2, 519–543. http://dx.doi.org/10.1006/jfan.1994.1078 Google Scholar
[2] Binding, P. A., Drabek, P., and Huang, Y. X., On Neumann boundary problems for some quasilinear elliptic equations. Electron. J. Differential Equations 5(1997), no. 05.Google Scholar
[3] Bozhkov, Y. and Mitidieri, E., Existence of multiple solutions for quasilinear systems viafibering method. J. Differential Equations 190(2003), no. 1, 239–267. http://dx.doi.org/10.1016/SOO22-O396(O2)OO112-2 Google Scholar
[4] Brock, E., Iturriaga, L., Sanchez, J. S., and Ubilla, P., Existence of positive solutions for p-Laplacian problems with weights. Commun. Pure and Appl. Anal. 5(2006), no. 4, 941–952. http://dx.doi.org/10.3934/cpaa.2006.5.941 Google Scholar
[5] Brown, K. J. and Zhang, Y., The Nehari manifold for a semilinear elliptic equation with a sign-changing weight function. J. Differential Equations 193(2003), no. 2, 481–499. http://dx.doi.org/10.101 6/S0022-0396(03)00121-9 Google Scholar
[6] Caffarelli, L., Kohn, R., Nirenberg, L., First order interpolation inequalities with weights. Compositio Math. 53(1984), no. 3, 259–275.Google Scholar
[7] Chen, C.-Y., Kuo, Y.-C., Wu, T.-F., TheNehari manifold for a Kirchhoff type problem involving sign-changing weight functions. J. Differential Equations. 250(2011), no. 4, 1876–1908. http://dx.doi.org/10.101 6/j.jde.2O10.11.01 7 Google Scholar
[8] Chen, S.-J. and Li, L., Multiple solutions for the nonhomogeneous Kirchhoff equation on HN. Nonlinear Anal. Real World Appl. 14(2013), no. 3, 1477–1486. http://dx.doi.org/10.1016/j.nonrwa.2012.10.010 Google Scholar
[9] Chipot, M. and Lovat, B., Some remarks on nonlocal elliptic and parabolic problems.Proceedings of the Second World Congress of Nonlinear Analysts, Part 7 (Athens, 1996).Nonlinear Anal. 30(1997),no. 7, 4619–4627. http://dx.doi.org/10.1016/S0362-546X(97)00169-7 Google Scholar
[10] Corrêa, F. J. S. A., On positive solutions of nonlocal and nonvariational elliptic problems. Nonlinear Anal. 59(2004), no. 7, 1147–1155. http://dx.doi.org/10.1016/j.na.2004.08.010 Google Scholar
[11] de Thélinand, K. J. Vélin, Existence and non-existence of nontrivial solution for some nonlinear elliptic systems. Rev. Mat. Univ. Complutense Madrid 6(1993), no. 1, 153–194.Google Scholar
[12] DiBenedetto, E., Degenerate parabolic equations. Universitext, Springer-Verlag, New York, 1993. http://dx.doi.org/10.1007/978-1-4612-0895-2 Google Scholar
[13] Drabek, P. and Pohozaev, S. I., Positive solutions for the p-Laplacian: application of the fibering method. Proc. Roy. Soc. Edinburgh Sect. A 127(1997), no. 4, 703–726. http://dx.doi.org/10.1017/S0308210500023787 Google Scholar
[14] Ekeland, I., On the variationalprinciple. J. Math. Anal. Appl. 47(1974,) 324–353. http://dx.doi.org/10.1016/0022-247X(74)90025-0 Google Scholar
[15] Kristalyand, A. Varga, C., Multiple solutions for a degenerate elliptic equation involving sublinear terms at infinity. J. Math. Anal. Appl. 352(2009), no. 1, 139–148. http://dx.doi.org/10.1016/j.jmaa.2008.03.025 Google Scholar
[16] Mitidieri, E., Sweers, G., R. van der Vorst, Non-existence theorems for systems of quasilinear partial defferential equations. Differential Integral Equations 8(1995), no. 6, 1331–1354.Google Scholar
[17] Miyagakiand, O. H. Rodrigues, R. S., On positive solutions for a class of singular quasilinear elliptic systems. J. Math. Anal. Appl. 334(2007), no. 2, 818–833. http://dx.doi.org/10.1016/j.jmaa.2007.01.018 Google Scholar
[18] Nehari, Z., On a class of nonlinear second-order differential equations. Trans. Amer. Math. Soc. 95(1960), 101–123. http://dx.doi.org/10.1090/S0002-9947-1960-0111898-8 Google Scholar
[19] Ni, W.-M. and Takagi, I., On the shape of least energy solution to a Neumann problem. Comm. Pure Appl. Math. 44(1991), no. 7, 819–851. http://dx.doi.org/10.1OO2/cpa.3160440705 Google Scholar
[20] Rabinowitz, P. H., Minimax methods in criticalpoint theory with applications to different equations. CBMS Regional Conference Series in Mathematics, 65, American Mathematical Society, Providence, RI, 1986. http://dx.doi.org/10.1090/cbms/065 Google Scholar
[21] Wu, T.-F., Onsemilinear elliptic equations involving concave-convex nonlinearities and sign-changing weight function. J. Math. Anal. Appl. 318(2006), no. 1, 253–270. http://dx.doi.org/10.1016/j.jmaa.2005.05.057 Google Scholar
[22] Wu, T.-F., Multiplicity results for a semilinear elliptic equation involving sign-changing weight function. Rocky Mountain J. Math.39(2009), no. 3,995-1011.http://dx.doi.org/10.1216/RMJ-2009-39-3-995 Google Scholar
[23] Xiu, Z. H., Chen, C. S., and Huang, J. C., Existence of multiple solution for an elliptic system with sign-changing weight functions. J. Math. Anal. Appl. 395(2012), no. 2, 531–541. http://dx.doi.org/10.1016/j.jmaa.2012.05.059 Google Scholar
[24] Xuan, B., The solvability of quasilinearBrezis-Nirenberg-typeproblems with singular weights. Nonlinear Anal. 62(2005), no. 4, 703–725. http://dx.doi.org/10.1016/j.na.2OO5.O3.O95 Google Scholar