No CrossRef data available.
Article contents
Exceptional Covers of Surfaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Consider a finite morphism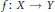 
$f\,:\,X\,\to \,Y$ of smooth, projective varieties over a finite field 
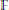$\mathbb{F}$. Suppose 
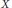$X$ is the vanishing locus in 
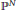${{\mathbb{P}}^{N}}$ of 
$r$ forms of degree at most 
$d$. We show that there is a constant 
$C$ depending only on 
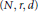$(N,\,r,\,d)$ and 
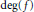$\deg (f)$ such that if 
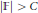$\left| \mathbb{F} \right|\,>\,C$, then 
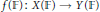$f\,(\mathbb{F})\,:\,X(\mathbb{F})\,\to Y(\mathbb{F})$ is injective if and only if it is surjective.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
[1] Cossec, F. R., Projective models of Enriques surfaces. Math. Ann.
265(1983), no. 3, 283–334. doi:10.1007/BF01456021Google Scholar
[2] Deligne, P., Cohomologie étale. In: Séminaire de Géométrie Algébrique du Bois-Marie SGA 4½, Lecture Notes in Mathematics 569, Springer-Verlag, New York, 1977.Google Scholar
[3] Deligne, P., La conjecture de Weil II. Inst. Hautes études Sci. Publ. Math.
52(1980), 137–252.Google Scholar
[4] Deligne, P. and Illusie, L., Relèvements modulo p
2
et décomposition du complexe de de Rham.
Invent. Math.
89(1987), no. 2, 247–270. doi:10.1007/BF01389078Google Scholar
[6] Guralnick, R. M., Tucker, T. J., and Zieve, M. E., Exceptional covers and bijections on rational points.
Int. Math. Res. No.
2007, no. 1, 20 pages.Google Scholar
[7] Kowalski, E., The large sieve, monodromy and zeta functions of curves. J. Reine Angew. Math.
601(2006), 29–69. doi:10.1515/CRELLE.2006.094Google Scholar
[8] Mumford, D., The canonical ring of an algebraic surface. Appendix to O. Zariski, The theorem of Riemann–Roch for high multiples of an effective divisor on an algebraic surface.
Ann. Math. (2)
76(1962), 612–615, 1962. doi:10.2307/1970376Google Scholar
[9] Poonen, B., Bertini theorems over finite fields. Ann. of Math. (2)
160(2004), no. 3, 1099–1127. doi:10.4007/annals.2004.160.1099Google Scholar
You have
Access