Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-05T16:39:50.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact Morphism Category and Gorenstein-projective Representations

Published online by Cambridge University Press:  20 November 2018

Xiu-Hua Luo
Xiu-Hua Luo*
Affiliation:
Department of Mathematics, Nantong University, Nantong 226019, P. R. China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

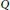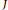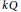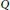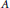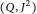Let $Q$ be a finite acyclic quiver, let $J$ be an ideal of $kQ$ generated by all arrows in $Q$, and let $A$ be a finite-dimensional $k$ -algebra. The category of all finite-dimensional representations of $\left( Q,\,{{J}^{2}} \right)$ over 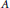$A$ is denoted by 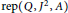$\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$ . In this paper, we introduce the category 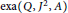$\text{exa}\left( Q,{{J}^{2}},A \right),$ which is a subcategory of 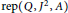$\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$ of all exact representations. The main result of this paper explicitly describes the Gorenstein-projective representations in 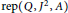$\text{rep}\left( Q,\,{{J}^{2}},\,A \right)$, via the exact representations plus an extra condition. As a corollary, 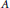$A$ is a self-injective algebra if and only if the Gorenstein-projective representations are exactly the exact representations of 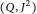$\left( Q,\,{{J}^{2}} \right)$ over 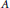$A$.

Keywords

18G25representation of a quiver over an algebraexact representationGorenstein-projective module
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 824 - 834
Copyright
Copyright © Canadian Mathematical Society 2015

References

[AB] Auslander, M. and Bridger, M., Stable module theory. Mem. Amer. Math. Soc, 94, American Mathematical Society, Providence, RI, 1969.Google Scholar
[AM] Avramov, L. L. and A. Martsinkovsky, Absolute, relative, and Tate cohomology of modules of finite Gorenstein dimension. Proc. London Math. Soc. 85(2002), no. 2, 393-440. http://dx.doi.Org/10.1112/S0024611 502013527 Google Scholar
[AR1] Auslander, M. and Reiten, I., Applications of contravariantly finite subcategories. Adv. Math. 86(1991), no. 1, 111–152. http://dx.doi.Org/10.1016/0001-8708(91)90037-8 Google Scholar
[AR2] Auslander, M. and Reiten, I., Cohen-Macaulay and Gorenstein artin algebras. In: Representation theory of finite groups and finite-dimensional algebras (Proc. Conf. at Bielefeld, 1991), Progr. Math., 95, Birkhâuser, Basel, 1991, pp. 221–245.Google Scholar
[ARS] Auslander, M., Reiten, I., and Smalo, S. O., Representation theory of Artin algebras. Cambridge Studies in Advanced Mathematics, 36, Cambridge University Press, Cambridge, 1995. http://dx.doi.Org/10.1017/CBO9780511623608 Google Scholar
[B] Beligiannis, A., Cohen-Macaulay modules, (co)torsion pairs and virtually Gorenstein algebras. J. Algebra 288(2005), no. 1, 137–211. http://dx.doi.Org/10.1016/j.jalgebra.2005.02.022 Google Scholar
[EJ1] Enochs, E. E. and O. M. G. Jenda, Gorenstein injective andprojective modules. Math. Z. 220(1995), no. 4, 611–633. http://dx.doi.Org/10.1007/BF02572634 Google Scholar
[EJ2] Enochs, E. E. and O. M. G. Jenda, Relative homological algebra, de Gruyter Expositions in Mathematics, 30, Walter de Gruyter Co., Berlin, 2000.Google Scholar
[GZ] Gao, N. and Zhang, P., Gorenstein derived categories. J. Algebra 323(2010), no. 7, 2041–2057. http://dx.doi.Org/10.1016/j.jalgebra.2O10.01.027 Google Scholar
[Hap] Happel, D., On Gorenstein algebras. In: Representation theory of finite groups and finite-dimensional algebras, Prog. Math., 95, Birkhaiiser, Basel, 1991, pp. 389–404.Google Scholar
[IKM] Iyama, O., Kato, K., and Miyachi, J. I., Recollement on homotopy categories and Cohen-Macaulay modules. J. K-Theory 8(2011), no. 3, 507–542. http://dx.doi.Org/10.1017/isOl1003007jkt143 Google Scholar
[LZ1] Li, Z. W. and P.Zhang, A construction of Gorenstein-projective modules. J. Algebra 323(2010), no. 6, 1802–1812. http://dx.doi.Org/1 0.101 6/j.jalgebra.2009.12.030 Google Scholar
[LZ2] Luo, X.-H. and P.Zhang, Monic representations and Gorenstein-projective modules. Pacific J. Math. 264(2013), no. 1, 163–194. http://dx.doi.Org/10.2140/pjm.2013.264.163 Google Scholar
[XZ] Xiong, B.-L. and Zhang, P., Gorenstein-projective modules over triangular matrix Artin algebras. J. Algebra Appl. 11(2012), no. 4, 1250066. http://dx.doi.Org/10.1142/S0219498812500661 Google Scholar
[Zl] Zhang, P., Monomorphism categories, cotilting theory, and Gorenstein-projective modules. J. Algebra 339(2011), 181–202. http://dx.doi.Org/10.1016/j.jalgebra.2011.05.018 Google Scholar
[Z2] Zhang, P., Gorenstein-projective modules and symmetric recollements. J. Algebra 388(2013), 65–80. http://dx.doi.Org/10.1016/j.jalgebra.2O13.05.008 Google Scholar