Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T19:12:52.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Every Real Algebraic Integer Is a Difference of Two Mahler Measures

Published online by Cambridge University Press:  20 November 2018

Paulius Drungilas  and
Artūras Dubickas
Paulius Drungilas
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, LT-03225 Vilnius, and, Institute of Mathematics and Informatics, Akademijos 4, LT-08663 Vilnius, Lithuania e-mail: [email protected]
Artūras Dubickas
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, LT-03225 Vilnius, Lithuania e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that every real algebraic integer 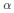$\alpha$ is expressible by a difference of two Mahler measures of integer polynomials. Moreover, these polynomials can be chosen in such a way that they both have the same degree as that of 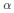$\alpha$, say 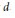$d$, one of these two polynomials is irreducible and another has an irreducible factor of degree 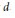$d$, so that 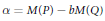$\alpha =M\left( P \right)-bM\left( Q \right)$ with irreducible polynomials 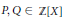$P,Q\in \mathbb{Z}\left[ X \right]$ of degree 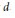$d$ and a positive integer $b$. Finally, if 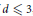$d\le 3$, then one can take 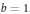$b=1$.

Keywords

11R0411R0611R0911R3311D09Mahler measuresPisot numbersPell equationabc-conjecture
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 191 - 195
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Adler, R. L. and Marcus, B., Topological entropy and equivalence of dynamical systems. Mem. Amer. Math. Soc. 20(1979), no. 219.Google Scholar
[2] Barbeau, E. J., Pell's equation. Springer-Verlag, New York, 2003.Google Scholar
[3] Boyd, D. W., Inverse problems for Mahler's measure. In: Diophantine Analysis. London Math. Soc. Lecture Note Ser. 109, Cambridge University Press, Cambridge, 1986, pp. 147–158.Google Scholar
[4] Boyd, D. W., Perron units which are not Mahler measures. Ergodic Theory Dynam. Systems 6(1986), no. 4, 485–488.Google Scholar
[5] Boyd, D. W., Reciprocal algebraic integers whose Mahler measures are non-reciprocal. Canad. Math. Bull. 30(1987), no. 1, 3–8.Google Scholar
[6] Dixon, J. D. and Dubickas, A., The values of Mahler measures. Mathematika 51(2004), no. 1–2, 131–148.Google Scholar
[7] Dubickas, A., Mahler measures close to an integer. Canad. Math. Bull. 45(2002), no. 2, 196–203.Google Scholar
[8] Dubickas, A., On numbers which are Mahler measures. Monatsh. Math. 141(2004), no. 2, 119–126.Google Scholar
[9] Dubickas, A., Mahler measures generate the largest possible groups. Math. Res. Lett. 11(2004), no. 2–3, 279–283.Google Scholar
[10] Dubickas, A., Mahler measures in a cubic field. Czechoslovak Math. J. 56(2006), no. 3, 949–956.Google Scholar
[11] Dubickas, A., Algebraic, arithmetic and geometric properties of Mahler measures. Proc. Inst. Math. (Nat. Acad. Sc. Belarus) 13(2005), 70–74.Google Scholar
[12] Dubickas, A. and Smyth, C. J., On the Remak height, the Mahler measure and conjugate sets of algebraic numbers lying on two circles. Proc. Edinburgh Math. Soc. 44(2001), no. 1, 1–17.Google Scholar
[13] Fan, A.-H. and Schmeling, J., ε-Pisot numbers in any real algebraic number field are relatively dense. J. Algebra 272(2004), no. 2, 470–475.Google Scholar
[14] Granville, A. and Tucker, T. J., It's as easy as abc. Notices Amer. Math. Soc. 49(2002), no. 10, 1224–1231.Google Scholar
[15] Salem, R., Algebraic numbers and Fourier analysis. D. C. Heath, Boston, MA, 1963.Google Scholar
[16] Schinzel, A., On values of the Mahler measure in quadratic field (solution of a problem of Dixon and Dubickas). Acta Arith. 113(2004), no. 4, 401–408.Google Scholar