Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T01:11:22.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Even Covering Properties and Somewhat Normal Spaces

Published online by Cambridge University Press:  20 November 2018

Hans-Peter Künzi  and
Peter Fletcher
Hans-Peter Künzi
Affiliation:
Universität BernCh-3012, Bern Switzerland
Peter Fletcher
Affiliation:
Virginia Tech, Blacksburg Virginia24061
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A topological space X is said to be somewhat normal provided that for each open cover 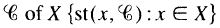is a normal cover of X. We show that a completely regular somewhat normal space need not be normal, thereby answering a question of W. M. Fleischman. We note that a collectionwise normal somewhat normal space need not be almost 2-fully normal, as had previously been asserted, and that neither the perfect image nor the perfect preimage of a somewhat normal space has to be somewhat normal.

Keywords

Primary54D18Secondary54D15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 29 , Issue 2 , 01 June 1986 , pp. 154 - 159
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Asanov, M.W., Properties that are close to paracompactness, Math. Zapeski 9 (1975), pp. 3—9. (Russian)Google Scholar
2. Cohen, H.J., Sur un problème de M. Dieudonné, C.R. Acad. Sri., Paris 234 (1952), pp. 290–292.Google Scholar
3. van Douwen, E., Hausdorff gaps and a nice countably paracompact nonnormal space, Topology Proc. 1 (1976), pp. 239–242.Google Scholar
4. Engelking, R., General Topology, Monografie Mat. 60, Polish Scientific Publishers, Warsaw, 1977.Google Scholar
5. Fleischman, W.M., A new extension of countable compactness, Fund. Math. 67 (1970), pp. 1—9.Google Scholar
6. Hart, K.P., Strong collectionwise normality and M. E. Rudin’ s Dowker space, Proc. Amer. Math. Soc. 83 (1981), pp. 802–806.Google Scholar
7. Kljusin, V.L., On spaces with regularly refinable coverings, Dokl. Akad. Nauk SSSR 204 (1972), pp. 782–783. Soviet Math. Dokl. 13 (1972), pp. 740-742.Google Scholar
8. Mack, J., On a class of countably paracompact spaces, Proc. Amer. Math. Soc. 16 (1965), pp. 467–472.Google Scholar
9. Mack, J.E. and Johnson, D.G., The Dedekind completion of C(X), Pacific J. Math. 20 (1967), pp. 231–243.Google Scholar
10. Michael, E., Point-finite and locally finite coverings, Canad. J. Math. 7 (1955), pp. 275–279.Google Scholar
11. Moore, R.L., Foundations of Point-set Theory, Amer. Math. Soc. Publ. No. 13, revised edition, 1962.Google Scholar
12. Shapiro, H.L. and Smith, F.A., Even covers and collectionwise normal spaces, Canad. J. Math. 30 (1978), pp. 466–473.Google Scholar
13. Shapiro, H.L. and Smith, F.A., Paracompactness in uniform spaces, Topology Proc. 3 (1978), pp. 179–197.Google Scholar
14. Shapiro, H.L. and Smith, F.A., Neighborhoods of the diagonal and strong normality properties, Proc. Amer. Math. Soc. 71 (1978), pp. 329–333.Google Scholar