Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T17:02:32.904Z Has data issue: false hasContentIssue false
  • English
  • Français

Essential Surfaces in Graph Link Exteriors

Published online by Cambridge University Press:  20 November 2018

Toru Ikeda
Toru Ikeda*
Affiliation:
Department of Mathematics, Kochi University, 2-5-1 Akebono-cho, Kochi 780-8520, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An irreducible graph manifold 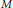$M$ contains an essential torus if it is not a special Seifert manifold. Whether 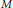$M$ contains a closed essential surface of negative Euler characteristic or not depends on the difference of Seifert fibrations from the two sides of a torus system which splits 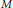$M$ into Seifert manifolds. However, it is not easy to characterize geometrically the class of irreducible graph manifolds which contain such surfaces. This article studies this problem in the case of graph link exteriors.

Keywords

57M25Graph linkGraph manifoldSeifert manifoldEssential surface
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 2 , 01 June 2009 , pp. 257 - 266
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Burde, G. and Murasugi, K., Links and Seifert fiber spaces. Duke Math. J. 37(1970), 89–93.Google Scholar
[2] Ikeda, T., Atoroidal decompositions of link exteriors. Kobe J. Math. 9(1992), no. 1, 71–88.Google Scholar
[3] Jaco, W., Lectures on three-manifold topology. CBMS Regional Conference Series in Mathematics 43, American Mathematical Society, Providence, RI, 1980.Google Scholar
[4] Jaco, W. and Shalen, P., Seifert fibered spaces in 3-manifolds. Mem. Amer. Math. Soc. 21(1979), no. 220.Google Scholar
[5] Johannson, K., Homotopy equivalences of 3-manifolds with boundaries. Lecture Notes in Mathematics 761, Springer, Berlin, 1979.Google Scholar