No CrossRef data available.
Article contents
Equations and Complexity for the Dubois–Efroymson Dimension Theorem
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $R$ be a real closed field, let
$R$ be a real closed field, let
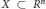 $X\,\subset \,{{R}^{n}}$ be an irreducible real algebraic set and let
$X\,\subset \,{{R}^{n}}$ be an irreducible real algebraic set and let 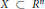 $Z$ be an algebraic subset of
$Z$ be an algebraic subset of 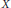 $X$ of codimension ≥ 2. Dubois and Efroymson proved the existence of an irreducible algebraic subset of
$X$ of codimension ≥ 2. Dubois and Efroymson proved the existence of an irreducible algebraic subset of 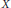 $X$ of codimension 1 containing
$X$ of codimension 1 containing 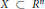 $Z$. We improve this dimension theorem as follows. Indicate by
$Z$. We improve this dimension theorem as follows. Indicate by  $\mu$ the minimum integer such that the ideal of polynomials in
$\mu$ the minimum integer such that the ideal of polynomials in
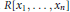 $R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
vanishing on
$R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
vanishing on 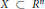 $Z$ can be generated by polynomials of degree
$Z$ can be generated by polynomials of degree 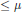 $\le \,\mu$. We prove the following two results: (1) There exists a polynomial
$\le \,\mu$. We prove the following two results: (1) There exists a polynomial
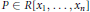 $P\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
of degree
$P\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
of degree 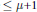 $\le \,\mu +1$ such that
$\le \,\mu +1$ such that
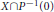 $X\cap {{P}^{-1}}\left( 0 \right)$
is an irreducible algebraic subset of
$X\cap {{P}^{-1}}\left( 0 \right)$
is an irreducible algebraic subset of 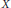 $X$ of codimension 1 containing
$X$ of codimension 1 containing 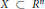 $Z$. (2) Let
$Z$. (2) Let  $F$ be a polynomial in
$F$ be a polynomial in
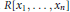 $R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
of degree
$R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
of degree  $d$ vanishing on
$d$ vanishing on 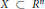 $Z$. Suppose there exists a nonsingular point
$Z$. Suppose there exists a nonsingular point  $x$ of
$x$ of 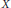 $X$ such that
$X$ such that 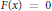 $F\left( x \right)\,=\,0$ and the differential at
$F\left( x \right)\,=\,0$ and the differential at  $x$ of the restriction of
$x$ of the restriction of  $F$ to
$F$ to 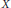 $X$ is nonzero. Then there exists a polynomial
$X$ is nonzero. Then there exists a polynomial
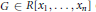 $G\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
of degree
$G\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$
of degree 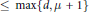 $\le \,\max \{d,\,\mu \,+\,1\}$ such that, for each
$\le \,\max \{d,\,\mu \,+\,1\}$ such that, for each 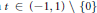 $t\,\in \,\left( -1,\,1 \right)\,\backslash \,\{0\}$, the set
$t\,\in \,\left( -1,\,1 \right)\,\backslash \,\{0\}$, the set 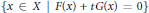 $\{x\in X|F\left( x \right)+tG\left( x \right)=0\}$ is an irreducible algebraic subset of
$\{x\in X|F\left( x \right)+tG\left( x \right)=0\}$ is an irreducible algebraic subset of 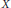 $X$ of codimension 1 containing
$X$ of codimension 1 containing 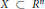 $Z$. Result (1) and a slightly different version of result (2) are valid over any algebraically closed field also.
$Z$. Result (1) and a slightly different version of result (2) are valid over any algebraically closed field also.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009


