Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T14:55:47.691Z Has data issue: false hasContentIssue false
  • English
  • Français

Envelope Dimension of Modules and the Simplified Radical Formula

Published online by Cambridge University Press:  20 November 2018

A. Nikseresht  and
A. Azizi
A. Nikseresht
Affiliation:
Department of Mathematics, College of Sciences, Shiraz University, 71457-44776, Shiraz, Iran e-mail: [email protected]@shirazu.ac.ir
A. Azizi
Affiliation:
Department of Mathematics, College of Sciences, Shiraz University, 71457-44776, Shiraz, Iran e-mail: [email protected]@shirazu.ac.ir
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce and investigate the notion of envelope dimension of commutative rings and modules over them. In particular, we show that the envelope dimension of a ring, $R$, is equal to that of the $R$-module 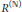${{\mathbb{R}}^{\left( \mathbb{N} \right)}}$. We also prove that the Krull dimension of a ring is no more than its envelope dimension and characterize Noetherian rings for which these two dimensions are equal. Moreover, we generalize and study the concept of simplified radical formula for modules, which we defined in an earlier paper.

Keywords

13A9913C9913C1313E05envelope dimensionsimplified radical formulaprime submodule
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 683 - 694
Copyright
Copyright © Canadian Mathematical Society 2013

Footnotes

The first author is partially funded by the National Elite Foundation.

References

[1] Atiyah, M. F. and Macdonald, I. G., Introduction to commutative algebra. Addison-Wesley, Reading, Mass.-London-Don Mills, Ont., 1969.Google Scholar
[2] Atiyah, M. F. and Macdonald, I. G., Radical formula and prime submodules. J. Algebra 307 (2007), no. 1, 454–460. http://dx.doi.org/10.1016/j.jalgebra.2006.07.006 Google Scholar
[3] Atiyah, M. F. and Macdonald, I. G., Radical formula and weakly prime submodules. Glasg. Math. J. 51 (2009), no. 2, 405–412. http://dx.doi.org/10.1017/S0017089509005072 Google Scholar
[4] Azizi, A. and Nikseresht, A., Simplified radical formula in modules. Houston J. Math. 38 (2012), no. 2, 333–344. http://dx.doi.org/10.1017/S0017089511000243 Google Scholar
[5] Behboodi, M., On weakly prime radical of modules and semi-compatible modules. Acta. Math. Hungar. 113 (2006), no. 3, 243–254. http://dx.doi.org/10.1007/s10474-006-0097-6 Google Scholar
[6] Behboodi, M. and Koohy, H., Weakly prime modules. Vietnam J. Math. 32 (2004), no. 2, 185–195.Google Scholar
[7] Huckaba, J. A., Commutative rings with zero divisors. Marcel Dekker, New York, 1988.Google Scholar
[8] Larsen, M. D. and McCarthy, P. J., Multiplicative theory of ideals. Pure and Applied Mathematics, 43, Academic Press, New York-London, 1971.Google Scholar
[9] Leung, K. H. and Man, S. H., On commutative Noetherian rings which satisfy the radical formula. Glasgow Math. J. 39 (1997), no. 3, 285–293. http://dx.doi.org/10.1017/S0017089500032225 Google Scholar
[10] Matsumura, H., Commutative ring theory. Cambridge Studies in Advanced Mathematics, 8, Cambridge University Press, Cambridge, 1986.Google Scholar
[11] McCasland, R. L. and Moore, M. E., On radicals of submodules of finitely generated modules. Canad. Math. Bull. 29 (1986), 37–39. http://dx.doi.org/10.4153/CMB-1986-006-7 Google Scholar
[12] Nikseresht, A. and Azizi, A., On arithmetical rings and the radical formula. Vietnam J. Math. 38 (2010), no. 1, 55–62.Google Scholar
[13] Nikseresht, A. and Azizi, A., Prime bases of weakly prime submodules and the weak radical of submodules. http://home.shirazu.ac.ir/_aazizi/MyFiles/Prime.pdfGoogle Scholar
[14] Sharif, H., Sharifi, Y., and Namazi, S., Rings satisfying the radical formula. Acta Math. Hungar. 71 (1996), no. 1–2, 103–108. http://dx.doi.org/10.1007/BF00052198 Google Scholar