Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T07:07:53.360Z Has data issue: false hasContentIssue false
  • English
  • Français

Enumerating Unlabelled Embeddings of Digraphs

Published online by Cambridge University Press:  20 November 2018

Yichao Chen ,
Xiaojian Gao  and
Yuanqiu Huang
Yichao Chen
Affiliation:
Department of Mathematics, Hunan University, 410082 Changsha, China e-mail: [email protected]
Xiaojian Gao
Affiliation:
Department of Mathematics, Hunan University, 410082 Changsha, China e-mail: [email protected]
Yuanqiu Huang
Affiliation:
Department of Mathematics, Normal University of Hunan, 410081 Changsha, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A 2-cell embedding of an Eulerian digraph 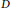$D$ into a closed surface is said to be directed if the boundary of each face is a directed closed walk in 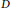$D$. In this paper, a method is developed with the purpose of enumerating unlabelled embeddings for an Eulerian digraph. As an application, we obtain explicit formulas for the number of unlabelled embeddings of directed bouquets of cycles 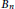${{B}_{n}}$, directed dipoles 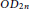$O{{D}_{2n}}$ and for a class of regular tournaments 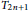${{T}_{2n+1}}$.

Keywords

05C10Eulerian digraphdirected embeddingunlabelled embedding
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 1 , 01 March 2018 , pp. 55 - 69
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bonetta-Martin, K. and McCourt, T. A., On which groups can arise as the canonical group of a spherical latin bitrade. Ars Math. Contemp. 13 (2017), 167–185.Google Scholar
[2] Bonnington, C. P., Conder, M., Morton, M., and McKenna, P., Embedding digraphs on orientable surfaces. J. Combin. Theory Ser. B 85 (2002), 1–20. http://dx.doi.Org/10.1OO6/jctb.2OO1.2085.Google Scholar
[3] Chen, Y., Gross, J. L., and Hu, X., Enumeration of digraph embeddings. European J. Combin. 36 (2014), 660–678. http://dx.doi.Org/10.1016/j.ejc.2013.10.003.Google Scholar
[4] Farr, G. E., Minorsfor alternating dimaps. arxiv:1311.2783.Google Scholar
[5] Feng, Y.-Q., Kwak, J.-H., and Zhou, J., Congruence classes of orientable 2-cell embeddings of bouquets of circles and dipoles. Electron. J. Combin. 17(2010), Research Paper 41,15.Google Scholar
[6] Kwak, J. H. and Lee, J., Enumeration of graph embeddings. Discrete Math. 135 (1994), 129–151. http://dx.doi.org/10.1016/0012-365X(93)E0075-FGoogle Scholar
[7] Kim, J. H. and Park, Y. K., Incongruent embeddings ofa bouquet into surfaces. Bull. Austral. Math. Soc. 61 (2000), 89–96. http://dx.doi.org/10.1017/S0004972700022048.Google Scholar
[8] Kim, J. H., Kim, H. K., and Lim, D. K., Enumerating embeddings of a dartboard graph into surfaces. Comm. Korean Math. Soc. 11 (1996), 1095–1104.Google Scholar
[9] McCourt, T. A., Growth rates ofgroups associated withface 2-coloured triangulations and directed eulerian digraphs on the sphere. Electron. J. Combin. 23(2016), no. 1, Paper 1.51, 23.Google Scholar
[10] McKay, B. D., The asymptotic numbers of regulär tournaments, Eulerian digraphs and Eulerian orientedgraphs. Combinatorica 10 (1990), 367–377. http://dx.doi.org/10.1007/BF02128671.Google Scholar
[11] Moon, J. W., Tournaments with a given automorphism group. Canad. J. Math. 16 (1964), 485–489. http://dx.doi.Org/10.41 53/CJM-1964-050-9.Google Scholar
[12] Mull, B. M., Enumerating the orientable 2-cell imbeddings ofcomplete bipartite graphs. J. Graph “Iheory 103 (1999), 77–90. http://dx.doi.Org/10.1002/(SICI)1097-011 8(1 99902)30:2<77::AID-JCT2>3.0.CO;2-W3.0.CO;2-W>Google Scholar
[13] Mull, B. M., Rieper, R. G., and White, A. T., Enumerating 2-cell imbeddings of connected graphs. Proc. Amer. Math. Soc. 103 (1988), 321–330. http://dx.doi.Org/10.2307/2047573.Google Scholar
[14] Tutte, W. T., The dissection of equilateral triangles into equilateral triangles. Proc. Cambridge Phil. Soc. 44 (1948), 463–482. http://dx.doi.Org/10.1017/S030500410002449XGoogle Scholar
[15] Tutte, W. T., Duality and trinity. Infinite andfinite sets (Colloq., Keszthely, 1973; dedicated to P. Erdös on his 60th birthday), Vol. III. Colloq. Math. Soc. Jänos Bolyai, 10, North-Holland, Amsterdam, 1975, pp. 1459-1472.Google Scholar