Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T06:49:06.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Endomorphisms of Two Dimensional Jacobians and Related Finite Algebras

Published online by Cambridge University Press:  20 November 2018

William Butske
William Butske*
Affiliation:
Department of Mathematics, Rose-Hulman Institute of Technology, Terre Haute, IN 47907, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Zarhin proves that if 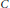$C$ is the curve 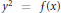${{y}^{2}}\,=\,f(x)$ where 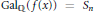$\text{Ga}{{\text{l}}_{\mathbb{Q}}}(f(x))\,=\,{{S}_{n}}$ or 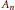${{A}_{n}}$, then 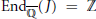$\text{En}{{\text{d}}_{\overline{\mathbb{Q}}}}(J)\,=\,\mathbb{Z}$. In seeking to examine his result in the genus 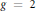$g\,=\,2$ case supposing other Galois groups, we calculate 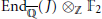$\text{En}{{\text{d}}_{\overline{\mathbb{Q}}}}(J)\,{{\otimes }_{\mathbb{Z}}}\,{{\mathbb{F}}_{2}}$ for a genus 2 curve where 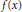$f(x)$ is irreducible. In particular, we show that unless the Galois group is ${{S}_{5}}$ or 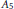${{A}_{5}}$, the Galois group does not determine 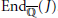$\text{En}{{\text{d}}_{\overline{\mathbb{Q}}}}(J)$.

Keywords

11G1020C20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 38 - 47
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] The GAP Group, GAP—Groups, Algorithms, and Programming, Version 4.4. http://www.gap-system.org, 2004.Google Scholar
[2] Lockhart, P., On the discriminant of a hyperelliptic curve. Trans. Amer. Math. Soc. 342(1994), no. 2, 729–752. doi:10.2307/2154650Google Scholar
[3] Mori, S., The endomorphism rings of some Abelian varieties. Japan. J. Math. (N.S.) 2(1976), no. 1, 109–130.Google Scholar
[4] Mumford, D., Abelian varieties. Tata Institute of Fundamental Research Studies in Mathematics, 5, Oxford University Press, London, 1970.Google Scholar
[5] Serre, J.-P., Abelian ℓ-adic representations and elliptic curves. Revised reprint of the 1968 original. Research Notes in Mathematics, 7, A K Peters, Wellesley, MA, 1998.Google Scholar
[6] Zarhin, Y. G., Abelian varieties ℓ-adic representations and SL2 . Izv. Akad. Nauk SSSR Ser. Mat. 43(1979), no. 2, 294–308.Google Scholar
[7] Zarhin, Y. G., Hyperelliptic Jacobians without complex multiplication. Math. Res. Lett. 7(2000), no. 1, 123–132.Google Scholar