Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T09:04:06.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalues of −Δp − Δq Under Neumann Boundary Condition

Published online by Cambridge University Press:  20 November 2018

Mihai Mihăilescu  and
Gheorghe Moroşanu
Mihai Mihăilescu
Affiliation:
Department of Mathematics, University of Craiova, 200585 Craiova, Romania and Research group of the project PN-II-ID-PCE-2012-4-0021, “Simion Stoilow” Institute of Mathematics of the Romanian Academy, 010702 Bucharest, Romania e-mail: [email protected]
Gheorghe Moroşanu
Affiliation:
Department of Mathematics and its Applications, Central European University, 1051 Budapest, Hungary e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The eigenvalue problem 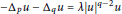$-{{\Delta }_{p}}u-{{\Delta }_{q}}u=\lambda {{\left| u \right|}^{q-2}}u$ with 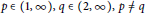$p\,\in \,\left( 1,\,\infty \right),\,q\,\in \,\left( 2,\,\infty \right),\,p\ne \,q$ subject to the corresponding homogeneous Neumann boundary condition is investigated on a bounded open set with smooth boundary from 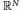${{\mathbb{R}}^{N}}$ with 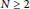$N\,\ge \,2$. A careful analysis of this problem leads us to a complete description of the set of eigenvalues as being a precise interval 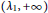$\left( {{\lambda }_{1,}}+\infty \right)$ plus an isolated point 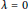$\lambda \,=\,0$. This comprehensive result is strongly related to our framework, which is complementary to the well-known case 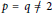$p\,=\,q\,\ne \,2$ for which a full description of the set of eigenvalues is still unavailable.

Keywords

35J6035J9246E3049R05eigenvalue problemSobolev spaceNehari manifoldvariational methods
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 606 - 616
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Badiale, M. and Serra, E., Semilinearelliptic equations for beginners.Existence results via the variational approach. Universitext, Springer, London, 2011. http://dx.doi.org/10.1007/978-0-85729-227-8 Google Scholar
[2] Brezis, H., Functional analysis, Sobolevspaces and partial differential equations. Universitext, Springer, New York, 2011.Google Scholar
[3] Casas, E. and Fernandez, L. A., A Green's formula for quasilinear elliptic operators.J. Math. Anal. Appl. 142(1989), no. 1, 62–73. http://dx.doi.org/10.1016/0022-247X(89)90164-9 Google Scholar
[4] Fărcăşeanu, M., Mihăilescu, M., and Stancu-Dumitru, D., On the set of eigenvalues of some PDEs with homogeneous Neumann boundary condition. Nonlinear Anal. 116(2015), 19–25. http://dx.doi.org/1 0.101 6/j.na.2O14.12.01 9 Google Scholar
[5] Gasinski, L. and Papageorgiou, N. S., Nonlinear analysis.Series in Mathematical Analysis and Applications, 9, Chapman & Hall/CRC, Boca Raton, FL, 2006.Google Scholar
[6] Le, A., Eigenvalue problems for p-Laplacian. Nonlinear Anal. 64(2006), no. 5,1057-1099. http://dx.doi.org/10.1016/j.na.2005.05.056 Google Scholar
[7] Mihăilescu, M., An eigenvalue problem possessing a continuous family of eigenvalues plus an isolated eigenvalue. Commun. Pure and Appl. Anal. 10(2011), 701–708. http://dx.doi.org/10.3934/cpaa.2011.10.701 Google Scholar
[8] Papageorgiou, N. S. and S. Th. Kyritsi-Yiallourou, Handbook on applied analysis.Advances in Mechanics and Mathematics, 19, Springer, New York, 2009.http://dx.doi.org/10.1007/b120946 Google Scholar
[9] Struwe, M., Variational methods: Applications to nonlinear partial differential equations and Hamiltonian systems.Ergebnisse der Mathematik und ihrerGrenzgebiete(3), 34, Springer-Verlag, Berlin, 1996. http://dx.doi.org/10.1007/978-3-662-03212-1 Google Scholar
[10] linesc, C., Mathematical programming in infinite dimensional normed spaces.(Romanian), Editura Academiei, Bucharest, 1998.Google Scholar