Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Coskun, Izzet
Harris, Joe
and
Starr, Jason
2009.
The Ample Cone of the Kontsevich Moduli Space.
Canadian Journal of Mathematics,
Vol. 61,
Issue. 1,
p.
109.
Chen, Dawei
2010.
Covers of elliptic curves and the moduli space of stable curves.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 649,
Chen, Dawei
and
Coskun, Izzet
2010.
Stable base locus decompositions of Kontsevich moduli spaces.
Michigan Mathematical Journal,
Vol. 59,
Issue. 2,
DeLand, Matthew
2011.
Complete Families of Linearly Non-degenerate Rational Curves.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 3,
p.
430.
Jensen, David
2012.
Rational fibrations of M¯5,1 and M¯6,1.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 3,
p.
633.
Giansiracusa, Noah
Jensen, David
and
Moon, Han-Bom
2013.
GIT compactifications ofM0,nand flips.
Advances in Mathematics,
Vol. 248,
Issue. ,
p.
242.
Gibney, Angela
Jensen, David
Moon, Han-Bom
and
Swinarski, David
2013.
Veronese quotient models of ̅M0,n and conformal blocks.
Michigan Mathematical Journal,
Vol. 62,
Issue. 4,
Manolache, Cristina
2014.
Stable maps and stable quotients.
Compositio Mathematica,
Vol. 150,
Issue. 9,
p.
1457.
Cooper, Yaim
2015.
The geometry of stable quotients in genus one.
Mathematische Annalen,
Vol. 361,
Issue. 3-4,
p.
943.
Moon, Han-Bom
and
Yoo, Sang-Bum
2016.
Birational Geometry of the Moduli Space of Rank 2 Parabolic Vector Bundles on a Rational Curve.
International Mathematics Research Notices,
Vol. 2016,
Issue. 3,
p.
827.
Fulger, Mihai
and
Murayama, Takumi
2022.
New constructions of nef classes on self-products of curves.
Mathematische Zeitschrift,
Vol. 302,
Issue. 2,
p.
1239.
Corniani, Elsa
and
Massarenti, Alex
2022.
Complete symplectic quadrics and Kontsevich spaces of conics in Lagrangian Grassmannians.
Advances in Mathematics,
Vol. 397,
Issue. ,
p.
108205.
Casarotti, Alex
Corniani, Elsa
and
Massarenti, Alex
2023.
Complete Singular Collineations and Quadrics.
International Mathematics Research Notices,
Vol. 2023,
Issue. 18,
p.
15370.
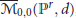 ${{\overline{M}}_{0,0}}\left( {{\mathbb{P}}^{r}},\,d \right)$
, stabilize when
${{\overline{M}}_{0,0}}\left( {{\mathbb{P}}^{r}},\,d \right)$
, stabilize when  $r\,\ge \,d$. We give a complete characterization of the effective divisors on
$r\,\ge \,d$. We give a complete characterization of the effective divisors on
 ${{\overline{M}}_{0,0}}\left( {{\mathbb{P}}^{d}},\,d \right)$
. They are non-negative linear combinations of boundary divisors and the divisor of maps with degenerate image.
${{\overline{M}}_{0,0}}\left( {{\mathbb{P}}^{d}},\,d \right)$
. They are non-negative linear combinations of boundary divisors and the divisor of maps with degenerate image.