Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T22:31:53.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Duality of Preenvelopes and Pure InjectiveModules

Published online by Cambridge University Press:  20 November 2018

Zhaoyong Huang
Zhaoyong Huang*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, Jiangsu Province, P. R. China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 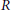$R$ be an arbitrary ring and let 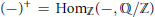${{\left( - \right)}^{+}}\,=\,\text{Ho}{{\text{m}}_{\mathbb{Z}}}\left( -,\,{\mathbb{Q}}/{\mathbb{Z}}\; \right)$, where 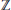$\mathbb{Z}$ is the ring of integers and 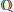$\mathbb{Q}$ is the ring of rational numbers. Let 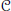$\mathcal{C}$ be a subcategory of left 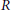$R$-modules and 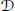$\mathcal{D}$ a subcategory of right 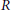$R$-modules such that 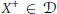${{X}^{+}}\,\in \,\mathcal{D}$ for any 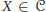$X\,\in \,\mathcal{C}$ and all modules in 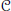$\mathcal{C}$ are pure injective. Then a homomorphism 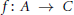$f:\,A\to \,C$ of left 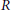$R$-modules with 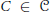$C\,\in \,\mathcal{C}$ is a 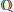$\mathcal{C}$-(pre)envelope of 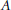$A$ provided 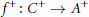${{f}^{+}}:\,{{C}^{+}}\,\to \,{{A}^{+}}$ is a 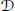$\mathcal{D}$-(pre)cover of 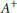${{A}^{+}}$. Some applications of this result are given.

Keywords

18G2516E30(pre)envelopes(pre)coversdualitypure injective modulescharacter modules
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 318 - 325
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

This research was partially supported by the Specialized Research Fund for the Doctoral Program of Higher Education (Grant No. 20100091110034), NSFC (Grant No. 11171142), NSF of Jiangsu Province of China (Grant Nos. BK2010047, BK2010007) and a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions

References

[AF] Anderson, F.W. and Fuller, K. R., Rings and categories of modules. Graduate Texts in Mathematics, 13, Springer-Verlag, New York, 1992.Google Scholar
[AsM] Asensio Mayor, J. and Martĭnez Hernández, J., On flat projective envelopes. J. Algebra 160 (1993, no. 2, 434–440.http://dx.doi.org/10.1006/jabr.1993.1195 CrossRefGoogle Scholar
[AuS] Auslander, M. and Smalø, S. O., Preprojective modules over artin algebras. J. Algebra 66 (1980, no. 1, 61–122.http://dx.doi.org/10.1016/0021-8693(80)90113-1 Google Scholar
[B1] Beligiannis, A., Cohen-Macaulay modules, (co)torsion pairs and virtually Gorenstein algebras. J. Algebra 288 (2005, no. 1, 137–211.http://dx.doi.org/10.1016/j.jalgebra.2005.02.022 CrossRefGoogle Scholar
[B2] Beligiannis, A., On algebras of finite Cohen-Macaulay type. Adv. Math. 226 (2011, no. 2, 1973–2019.http://dx.doi.org/10.1016/j.aim.2010.09.006 Google Scholar
[CS] Cheatham, T. J. and Stone, D. R., Flat and projective character modules. Proc. Amer. Math. Soc. 81 (1981, no. 2, 175–177.http://dx.doi.org/10.1090/S0002-9939-1981-0593450-2 Google Scholar
[DC] Ding, N. Q. and Chen, J. L., Relative coherence and pre-envelopes. Manuscripta Math. 81 (1993, no. 3–4, 243–262.http://dx.doi.org/10.1007/BF02567857 CrossRefGoogle Scholar
[E] Enochs, E. E., Injective and flat covers, envelopes and resolvents. Israel J. Math. 39 (1981, no. 3, 189–209.http://dx.doi.org/10.1007/BF02760849 CrossRefGoogle Scholar
[EH] Enochs, E. E. and Huang, Z. Y., Injective envelopes and (Gorenstein) flat covers. Algebr. Represent. Theory 15 (2012, no. 6, 1131–1145.http://dx.doi.org/10.1007/s10468-011-9282-6 Google Scholar
[EJ1] Enochs, E. E. and Jenda, O. M. G., Gorenstein injective and projective modules. Math. Z. 220 (1995, no. 4, 611–633.http://dx.doi.org/10.1007/BF02572634 CrossRefGoogle Scholar
[EJ2] Enochs, E. E. and Jenda, O. M. G., Relative homological algebra, Vol. 1. Second Ed., de Gruyter Expositions in Mathematics, 30, Walter de Gruyter, Berlin, Berlin, 2011.Google Scholar
[F] Fieldhouse, D. J., Character modules. Comment. Math. Helv. 46 (1971, 274–276.http://dx.doi.org/10.1007/BF02566844 CrossRefGoogle Scholar
[G] Glaz, S., Commutative coherent rings. Lecture Notes in Mathematics, 1371, Springer-Verlag, Berlin, 1989.Google Scholar
[GT] Göbel, R. and Trlifaj, J., Approximations and endomorphism algebras of modules. de Gruyter Expositions in Mathematics, 41, Walter de Gruyter GmbH & Co. KG, Berlin, 2006.Google Scholar
[H] Holm, H., Gorenstein homological dimensions. J. Pure Appl. Algebra 189 (2004, no. 1–3, 167–193.http://dx.doi.org/10.1016/j.jpaa.2003.11.007 Google Scholar
[HuX] Hu, J. S. and Xu, A. M., On stability of F-Gorenstein flat categories. Algebra Colloq., to appear.Google Scholar
[K] Krause, H., The spectrum of a module category. Mem. Amer. Math. Soc. 149 (2001, no. 707.Google Scholar
[M] Matlis, E., Injective modules over Noetherian rings. Pacific J. Math. 8 (1958, 511–528.http://dx.doi.org/10.2140/pjm.1958.8.511 CrossRefGoogle Scholar
[Me] Megibben, C., Absolutely pure modules. Proc. Amer. Math. Soc. 26 (1970, 561–566.http://dx.doi.org/10.1090/S0002-9939-1970-0294409-8 CrossRefGoogle Scholar
[P] Pinzon, K., Absolutely pure covers. Comm. Algebra 36 (2008, no. 6, 2186–2194.http://dx.doi.org/10.1080/00927870801952694 CrossRefGoogle Scholar
[SE] Sabbagh, G. and Eklof, P., Definability problems for rings and modules. J. Symbolic Logic 36 (1971, 623–649.http://dx.doi.org/10.2307/2272466 Google Scholar