Article contents
The Dual of the Compressed Shift
Published online by Cambridge University Press: 17 April 2020
Abstract
For an inner function u, we discuss the dual operator for the compressed shift 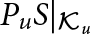 $P_u S|_{{\mathcal {K}}_u}$, where
$P_u S|_{{\mathcal {K}}_u}$, where 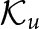 ${\mathcal {K}}_u$ is the model space for u. We describe the unitary equivalence/similarity classes for these duals as well as their invariant subspaces.
${\mathcal {K}}_u$ is the model space for u. We describe the unitary equivalence/similarity classes for these duals as well as their invariant subspaces.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
This work was partially supported by FTC/Portugal through the grant UID/MAT/04459/2019. The second author would like to thank the Center for Mathematical Analysis, Geometry, and Dynamical Systems for their hospitality where the initial research for this paper was done.
References
- 7
- Cited by



