Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T19:48:02.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisors on Varieties Over a Real Closed Field

Published online by Cambridge University Press:  20 November 2018

W. Kucharz
W. Kucharz*
Affiliation:
Department of Mathematics University of New Mexico Albuquerque, New Mexico 87131 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a projective nonsingular variety over a real closed field R such that the set X(R) of R-rational points of X is nonempty. Let ClR(X) = Cl(X)/Γ(X), where Cl(X) is the group of classes of linearly equivalent divisors on X and Γ(X) is the subgroup of Cl(X) consisting of the classes of divisors whose restriction to some neighborhood of X(R) in X is linearly equivalent to 0. It is proved that the group ClR(X) is isomorphic to (Z/2)s for some non-negative integer s. Moreover, an upper bound on s is given in terms of the Z/2-dimension of the group cohomology modules of Gal(C/R), where 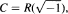, with values in the Néron-Severi group and the Picard variety of Xc = X xR C.

Keywords

14C2014P05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 4 , 01 December 1992 , pp. 503 - 509
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Becker, E., Valuations and real places in the theory of formally real fields. In: Géométrie Algébrique Réelle et Formes Quadratiques, Lecture Notes in Math. 959, Springer, 1982 1–40.Google Scholar
2. Bochnak, J., Coste, M. and Roy, M.-F., Géométrie Algébrique Réelle, Ergebnisse der Math., 12, Berlin, Heidelberg, New York, Springer Verlag, 1987.Google Scholar
3. Bröcker, L., Reelle Divisoren, Arch, der Math. 35(1980), 140–143.Google Scholar
4. Brumfiel, G. W., Partially Ordered Rings and Semi-algebraic Geometry, Cambridge Univ. Press, Cambridge, 1979.Google Scholar
5. Delfs, H. and Knebusch, M., Semi-algebraic topology over a real closed field I, II, Math. Z. 177(1981), 107–129; Math. Z. 178(1981), 175–213.Google Scholar
6. Delfs, H., On the homology of algebraic varieties over real closed fields, J. Reine Angew. Math. 335(1982), 122–163.Google Scholar
7. Evans, E. G., Projective modules as fiber bundles, Proc. Amer. Math. Soc. 27(1971), 623–626.Google Scholar
8. Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero, Ann. of Math. 79(1964), 109–326.Google Scholar
9. Knebusch, M., On algebraic curves over real closed fields I, Math Z. 150(1976), 49–70.Google Scholar
10. Lang, S. and A. Néron, Rational points of abelian varieties over function fields, Amer. J. Math. 81(1959), 95–118.Google Scholar
11. Serre, J.-P., Groups Algébriques et Corps de Classes, Hermann, Paris, 1959.Google Scholar
12. Silhol, R., Real Algebraic Surfaces, Lecture Notes in Math. 1392, Springer, 1989.Google Scholar
13. Swan, R. G., Topological examples of projective modules, Trans. Amer. Math. Soc. 230(1977), 201–234.Google Scholar