Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T15:40:24.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Discriminants of Complex Multiplication Fields of Elliptic Curves over Finite Fields

Published online by Cambridge University Press:  20 November 2018

Florian Luca  and
Igor E. Shparlinski
Florian Luca
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, C.P. 58089, Morelia, Michoacán, México e-mail: [email protected]
Igor E. Shparlinski
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that, for most of the elliptic curves 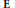$\text{E}$ over a prime finite field 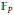${{\mathbb{F}}_{p}}$ of 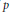$p$ elements, the discriminant 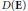$D\left( E \right)$ of the quadratic number field containing the endomorphism ring of 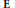$\text{E}$ over 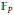${{\mathbb{F}}_{p}}$ is sufficiently large. We also obtain an asymptotic formula for the number of distinct quadratic number fields generated by the endomorphism rings of all elliptic curves over 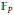${{\mathbb{F}}_{p}}$.

Keywords

11G2011N3211R11
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 409 - 417
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Avanzi, R., Cohen, H., Doche, C., Frey, G., Lange, T., Nguyen, K. and Vercauteren, F., Elliptic and Hyperelliptic Curve Cryptography: Theory and Practice. CRC Press, 2005.Google Scholar
[2] Cojocaru, A. and Duke, W., Reductions of an elliptic curve and their Tate-Shafarevich groups. Math. Ann. 329(2004), no. 3, 513–534.Google Scholar
[3] Cojocaru, A., Fouvry, E. and Murty, M. R., The square sieve and the Lang-Trotter conjecture. Canad. J. Math. 57(2005), no. 6, 1155–1178.Google Scholar
[4] Cutter, P., Granville, A. and Tucker, T. J., The number of fields generated by the square root of values of a given polynomial. Canad. Math. Bull. 46(2003), no. 1, 71–79.Google Scholar
[5] Deuring, M., Die Typen der Multiplikatorenringe elliptischer Funktionenkörper. Abh. Math. Sem. Hansischen Univ. 14(1941), 197–272.Google Scholar
[6] Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers. Fifth edition. Oxford University Press, New York, 1979.Google Scholar
[7] Huxley, M. N., A note on polynomial congruences. In: Recent Progress in Analytic Number Theory, Vol.1, Academic Press, London, 1981, pp. 193–196.Google Scholar
[8] Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
[9] Jao, D., Miller, S. D. and Venkatesan, R., Ramanujan graphs and the random reducibility of discrete log on isogenous elliptic curves. Preprint (available from http://arxiv.org/abs/math.NT/0411378), 2004.Google Scholar
[10] Lenstra, H. W. Jr., Factoring integers with elliptic curves. Annals of Math. 126(1987), no. 3, 649–673.Google Scholar
[11] Silverman, J. H., The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 106, Springer-Verlag, Berlin, 1995.Google Scholar
[12] Wirsing, E., Das asymptotische Verhalten von Summen über multiplikative Funktionen. Math. Ann. 143(1961), 75–102.Google Scholar