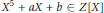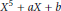Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Spearman, Blair K.
Williams, Kenneth S.
and
Yang, Qiduan
2007.
On the Common Index Divisors of a Dihedral Field of Prime Degree.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2007,
Issue. ,
p.
1.
Jones, Lenny
and
Phillips, Tristan
2018.
Infinite families of monogenic trinomials and their Galois groups.
International Journal of Mathematics,
Vol. 29,
Issue. 05,
p.
1850039.
Jones, Lenny
2022.
Monogenic reciprocal trinomials and their Galois groups.
Journal of Algebra and Its Applications,
Vol. 21,
Issue. 02,
Jakhar, Anuj
Kaur, Sumandeep
and
Khanduja, Sudesh K.
2023.
Discriminant and integral basis of quintic fields defined by x5 + ax + b.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 05,