Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-02T19:28:49.201Z Has data issue: false hasContentIssue false
  • English
  • Français

Diameter of a (0, 1)-Matrix*

Published online by Cambridge University Press:  20 November 2018

U.S.R. Murty
U.S.R. Murty*
Affiliation:
University of Waterloo Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an m×n (0, l )-matrix. Let C1, C2, …, Cn denote its columns. A sequence of distinct columns 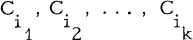is said to form a chain if the inner product of 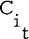and 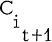(for 1 ≤ t ≤ k-l) is at least one. k-1 is called the length of the chain and this chain is said to connect 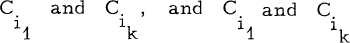are said to be connected. As can be easily seen, connectedness is an equivalence relation on the set of columns. A matrix is called connected if all its columns belong to the same equivalence class. If Ci and Cj belong to the same equivalence class, then s(Ci, Cj) will denote the length of the shortest chain between Ci and Cj We define the distance between any two columns Ci and Cj to be denoted by d(Ci, Cj), in the following manner.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 2 , June 1968 , pp. 285 - 288
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

*

This work was done while the author was at the University of Alberta, Edmonton.

References

1. Ryser, H. J., Combinatorial properties of matrices of zeros and ones. Canadian Journal of Mathematics, 9 (1957) 371-377.Google Scholar