Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kimberling, Clark
1981.
Almost Arithmetic Sequences and Complementary Systems.
The Fibonacci Quarterly,
Vol. 19,
Issue. 5,
p.
426.
de Bruijn, N.G.
1981.
Sequences of zeros and ones generated by special production rules.
Indagationes Mathematicae (Proceedings),
Vol. 84,
Issue. 1,
p.
27.
Kimberling, Clark
1981.
Fractional Parts (
nr
-
s
), Almost Arithmetic Sequences, And Fibonacci Numbers
.
The Fibonacci Quarterly,
Vol. 19,
Issue. 3,
p.
280.
Boshernitzan, M
and
Fraenkel, A.S
1984.
A linear algorithm for nonhomogeneous spectra of numbers.
Journal of Algorithms,
Vol. 5,
Issue. 2,
p.
187.
Aviram, I
1986.
The diffraction spectrum of a general family of linear quasiperiodic arrays.
Journal of Physics A: Mathematical and General,
Vol. 19,
Issue. 16,
p.
3299.
Werman, Michael
Wu, Angela Y.
and
Melter, Robert A.
1987.
Recognition and characterization of digitized curves.
Pattern Recognition Letters,
Vol. 5,
Issue. 3,
p.
207.
de Bruijn, N.G.
1989.
Updown generation of Beatty sequences.
Indagationes Mathematicae (Proceedings),
Vol. 92,
Issue. 4,
p.
385.
Fraenkel, A. S.
Porta, H.
and
Stolarsky, K. B.
1990.
Analytic Number Theory.
p.
255.
Bruckstein, A.M.
1990.
The self-similarity of digital straight lines.
Vol. i,
Issue. ,
p.
485.
Tognetti, Keith
Winley, Graham
and
van Ravenstein, Tony
1990.
Applications of Fibonacci Numbers.
p.
325.
Ravenstein, Tony van
Winley, Graham
and
Tognetti, Keith
1990.
Characteristics and the Three Gap Theorem.
The Fibonacci Quarterly,
Vol. 28,
Issue. 3,
p.
204.
Brown, Tom C.
and
Freedman, Allen R.
1991.
Some Sequences Associated with the Golden Ratio.
The Fibonacci Quarterly,
Vol. 29,
Issue. 2,
p.
157.
Bunder, Martin
and
Tognetti, Keith
1991.
The Zeckendorf Representation and the Golden Sequence.
The Fibonacci Quarterly,
Vol. 29,
Issue. 3,
p.
217.
Siegel, Ralph M.
Tresser, Charles
and
Zettler, George
1992.
A decoding problem in dynamics and in number theory.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 2,
Issue. 4,
p.
473.
Berstel, Jean
and
Séébold, Patrice
1993.
Mathematical Foundations of Computer Science 1993.
Vol. 711,
Issue. ,
p.
281.
Yamashita, Mamoru
1993.
Some Classes of Self-Similar Quasiperiodic Lattices with Uniformity.
Journal of the Physical Society of Japan,
Vol. 62,
Issue. 1,
p.
140.
Linderbaum, M.
and
Bruckstein, A.
1993.
On recursive, O(N) partitioning of a digitized curve into digital straight segments.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 15,
Issue. 9,
p.
949.
Chuan, Wai-fong
1993.
Applications of Fibonacci Numbers.
p.
113.
Fraenkel, A.S.
and
Kimberling, Clark
1994.
Generalized Wythoff arrays, shuffles and interspersions.
Discrete Mathematics,
Vol. 126,
Issue. 1-3,
p.
137.
Fraenkel, Aviezri S.
1994.
Iterated floor function, algebraic numbers, discrete chaos, Beatty subsequences, semigroups.
Transactions of the American Mathematical Society,
Vol. 341,
Issue. 2,
p.
639.


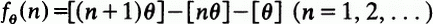 where [x] denotes the greatest integer not exceeding
where [x] denotes the greatest integer not exceeding 