Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:15:40.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Determination of Hauptmoduls and Construction of Abelian Extensions of Quadratic Number Fields

Published online by Cambridge University Press:  20 November 2018

Hung-Jen Chiang-Hsieh  and
Yifan Yang
Hung-Jen Chiang-Hsieh
Affiliation:
Department of Mathematics, National Chung Cheng University, Chiayi 621, Taiwan e-mail: [email protected]
Yifan Yang
Affiliation:
Department of Applied Mathematics, National Chiao Tung University, Hsinchu 300, Taiwan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain Hauptmoduls of genus zero congruence subgroups of the type 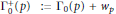$\Gamma _{0}^{+}\left( p \right)\,\,:={{\Gamma }_{0}}\left( p \right)+{{w}_{p}}$, where 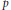$p$ is a prime and 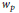${{w}_{p}}$ is the Atkin–Lehner involution. We then use the Hauptmoduls, along with modular functions on ${{\Gamma }_{1}}\left( p \right)$ to construct families of cyclic extensions of quadratic number fields. Further examples of cyclic extension of bi-quadratic and tri-quadratic number fields are also given.

Keywords

11F0311G1611R20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 334 - 346
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Conway, J. H. and Norton, S. P., Monstrous moonshine. Bull. London Math. Soc. 11(1979), no. 3, 308–339.Google Scholar
[2] Cox, D., McKay, J., and Stevenhagen, P., Principal moduli and class fields. Bull. LondonMath. Soc. 36(2004), no. 1, 3–12.Google Scholar
[3] Darmon, H., Note on a polynomial of Emma Lehmer. Math. Comp. 56(1991), no. 194, 795–800.Google Scholar
[4] Kubert, D. S. and Lang, Serge, Modular Units. Grundlehren der Mathematischen Wissenschaften 244, Springer-Verlag, New York, 1981.Google Scholar
[5] Lecacheux, O., Unités d’une famille de corps cycliques réeles de degré 6 liés à la courbe modulaire X 1(13) . J. Number Theory 31(1989), no. 1, 54–63.Google Scholar
[6] McKay, J. and Strauss, H., The q-series of monstrous moonshine and the decomposition of the head characters. Comm. Algebra 18(1990), no. 1, 253–278.Google Scholar
[7] Ogg, A. P., On theWeierstrass points of X 0 (N). Illinois J. Math. 22(1978), no. 1, 31–35.Google Scholar
[8] Washington, L. C., A family of cyclic quartic fields arising from modular curves. Math. Comp. 57(1991), no. 196, 763–775.Google Scholar
[9] Yang, Y., Defining equations of modular curves. Adv. Math. 204(2006), no. 2, 481–508.Google Scholar
[10] Yang, Y., Transformation formulas for generalized Dedekind eta functions. Bull. London Math. Soc. 36(2004), no. 5, 671–682.Google Scholar