Derivations Whose Iterates are Zero or Invertible On a Left Ideal

Abstract

Let n ∊ ℤ⁺ and R be a ring which possesses a unit element, a left ideal J, and a derivation d such that dⁿ(J) ≠ 0 and dⁿ(r) is 0 or invertible, for all r ∊ J. We prove that either R is primitive, in which case R is D_i with 1 ≤ i ≤ n+ 1, where D_i is the ring of i × i matrices over a division ring D, or else there exist positive integers i, l and p with p prime and 2 ≤ ip^l ≤ n + 1, such that R is 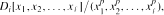where D is a division ring with characteristic p, and furthermore there is a derivation f of D_i and a₁, a₂,..,a_l ∊ Z_Di., the center of D_i, such that a ∊ D_i then

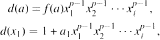
and

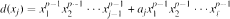
for all 2 ≤ j ≤ l