Derivations on Toeplitz Algebras

Abstract

Let 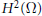${{H}^{2}}\left( \Omega \right)$ be the Hardy space on a strictly pseudoconvex domain $\Omega \,\subset \,{{\mathbb{C}}^{n}}$, and let 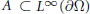$A\,\subset \,{{L}^{\infty }}\left( \partial \Omega \right)$ denote the subalgebra of all 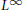${{L}^{\infty }}$-functions 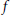$f$ with compact Hankel operator 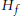${{H}_{f}}$. Given any closed subalgebra $B\,\subset \,A$ containing 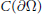$C\left( \partial \Omega \right)$, we describe the first Hochschild cohomology group of the corresponding Toeplitz algebra 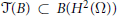$\mathcal{T}\left( B \right)\,\subset \,B\left( {{H}^{2}}\left( \Omega \right) \right)$. In particular, we show that every derivation on 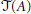$\mathcal{T}\left( A \right)$ is inner. These results are new even for $n\,=\,1$, where it follows that every derivation on 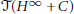$\mathcal{T}\left( {{H}^{\infty }}\,+\,C \right)$ is inner, while there are non-inner derivations on 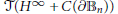$\mathcal{T}\left( {{H}^{\infty }}\,+\,C\left( \partial {{\mathbb{B}}_{n}} \right) \right)$ over the unit ball 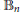${{\mathbb{B}}_{n}}$ in dimension 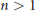$n\,>\,1$.